Bioethanol production optimization by direct numerical methods and evolutionary algorithms
Keywords:
Nonlinear system, Fourier series, optimal control, evolutionary algorithms, bioethanol productionAbstract
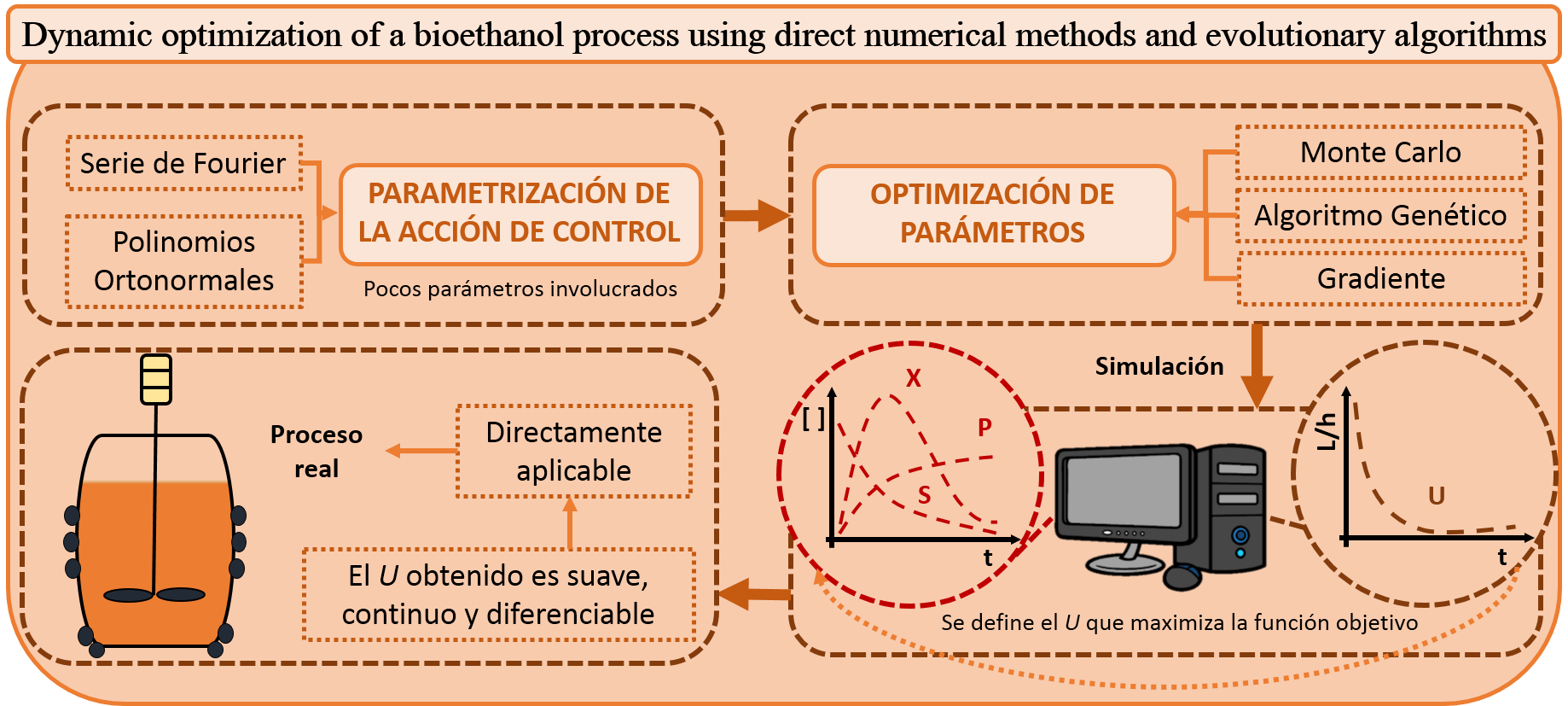
This paper develops a dynamic optimization methodology based on direct numerical methods, for the bioethanol fed-batch production from glucose and fructose as a substrate. The mathematical model that governs the process consists of six differential equations and is highly nonlinear. The proposed strategy uses the Fourier trigonometric basis and normalized orthogonal polynomials for substrate feeding rate parameterization. Then, evolutionary algorithms and gradient methods are combined to search parameters that generate the best control action. This parameterization methodology requires a minimum number of parameters to optimize. Also, the continuous and differentiable nature of the optimal profile enables its direct implementation in the physical process, eliminating the necessity for filtering or smoothing it. In addition, they are ideal for bioprocesses, in which it is preferable to avoid abrupt changes in the operating modes of the process to promote cell growth. As a result, using only 3 parameters, a 3.5% increase in ethanol production was achieved, while the reference uses at least 10 parameters and provides a stepped feed profile. The simulations have yielded promising results, making this proposal an alternative with excellent potential for process optimization.
Downloads
References
S. H. M. Azhar, R. Abdulla, S. A. Jambo, H. Marbawi, J. A. Gansau, A. A. M. Faik, and K. F. Rodrigues, “Yeasts in sustainable bioethanol production: A review,” Biochemistry and biophysics reports, vol. 10, pp. 52–61, 2017.
A. de Azevedo, F. Fornasier, M. da Silva Szarblewski, R. d. C. de Souza Schneider, M. Hoeltz, and D. de Souza, “Life cycle assessment
of bioethanol production from cattle manure,” Journal of cleaner production, vol. 162, pp. 1021–1030, 2017.
A. G. B. Ozdingis and G. Kocar, “Current and future aspects of bioethanol production and utilization in turkey,” Renewable and Sustainable Energy Reviews, vol. 81, pp. 2196–2203, 2018.
M. Vohra, J. Manwar, R. Manmode, S. Padgilwar, and S. Patil, “Bioethanol production: feedstock and current technologies,” Journal of Environmental Chemical Engineering, vol. 2, no. 1, pp. 573–584, 2014.
N. Nasir, W. R. W. Daud, S. Kamarudin, and Z. Yaakob, “Process system engineering in biodiesel production: A review,” Renewable and Sustainable Energy Reviews, vol. 22, pp. 631–639, 2013.
J. Lee, S. Y. Lee, S. Park, and A. P. Middelberg, “Control of fed-batch fermentations,” Biotechnology advances, vol. 17, no. 1, pp. 29–48, 1999.
S. Romoli, G. J. E. Scaglia, M. E. Serrano, S. A. Godoy, O. A. Ortiz, and J. R. Vega, “Control of a fed-batch fermenter based on a linear algebra strategy,” Latin America Transactions, IEEE (Revista IEEE America Latina), vol. 12, no. 7, pp. 1206–1213, 2014.
S. Ochoa, “A new approach for finding smooth optimal feeding profiles in fed-batch fermentations,” Biochemical engineering journal, vol. 105, pp. 177–188, 2016.
R. Luus, “Optimization of fed-batch fermentors by iterative dynamic programming,” Biotechnology and Bioengineering, vol. 41, no. 5, pp. 599–602, 1993.
S. Park and W. Fred Ramirez, “Optimal production of secreted protein in fed-batch reactors,” AIChE Journal, vol. 34, no. 9, pp. 1550–1558, 1988.
A. Arpornwichanop and N. Shomchoam, “Studies on optimal control approach in a fed-batch fermentation,” Korean Journal of Chemical Engineering, vol. 24, pp. 11–15, 2007.
J. Li and R. R. Rhinehart, “Heuristic random optimization,” Computers & chemical engineering, vol. 22, no. 3, pp. 427–444, 1998.
J. Zhang, “Developing robust neural network models by using both dynamic and static process operating data,” Industrial & engineering chemistry research, vol. 40, no. 1, pp. 234–241, 2001.
W.-H. Hunag, G. S. Shieh, and F.-S. Wang, “Optimization of fed-batch fermentation using mixture of sugars to produce ethanol,” Journal of the Taiwan Institute of Chemical Engineers, vol. 43, no. 1, pp. 1–8, 2012.
C. Fernández, N. Pantano, S. Godoy, E. Serrano, and G. Scaglia, “Optimización de parámetros utilizando los métodos de monte carlo y algoritmos evolutivos. aplicación a un controlador de seguimiento de trayectoria en sistemas no lineales,” Revista Iberoamericana de Automática e Informática industrial, vol. 16, no. 1, pp. 89–99, 2019.
M. C. Fernández, M. N. Pantano, R. A. F. Machado, O. A. Ortiz, and G. J. Scaglia, “Nonlinear multivariable tracking control: application to an ethanol process,” International Journal of Automation and Control, vol. 13, no. 4, pp. 440–468, 2019.
M. N. Pantano, M. C. Fernández, O. A. Ortiz, G. J. Scaglia, and J. R. Vega, “A fourier-based control vector parameterization for the
optimization of nonlinear dynamic processes with a finite terminal time,” Computers & Chemical Engineering, vol. 134, p. 106721, 2020.
E. Kreyszig, “Introductory functional analysis with applications. jonh wiley & sons,” Inc., New York, 1978.
R. K. Nagle, E. B. Saff, and A. D. Snider, Ecuaciones diferenciales y problemas con valores en la frontera. Pearson Educación, 2000.
F. L. Lewis, D. Vrabie, and V. L. Syrmos, Optimal control. John Wiley & Sons, 2012.