Set-membership affine projection algorithm based on the percentage change of the error signal and variable projection order

Authors

Keywords:

set-membership algorithm, affine projection algorithm, data selective algorithms, variable projection order

Abstract

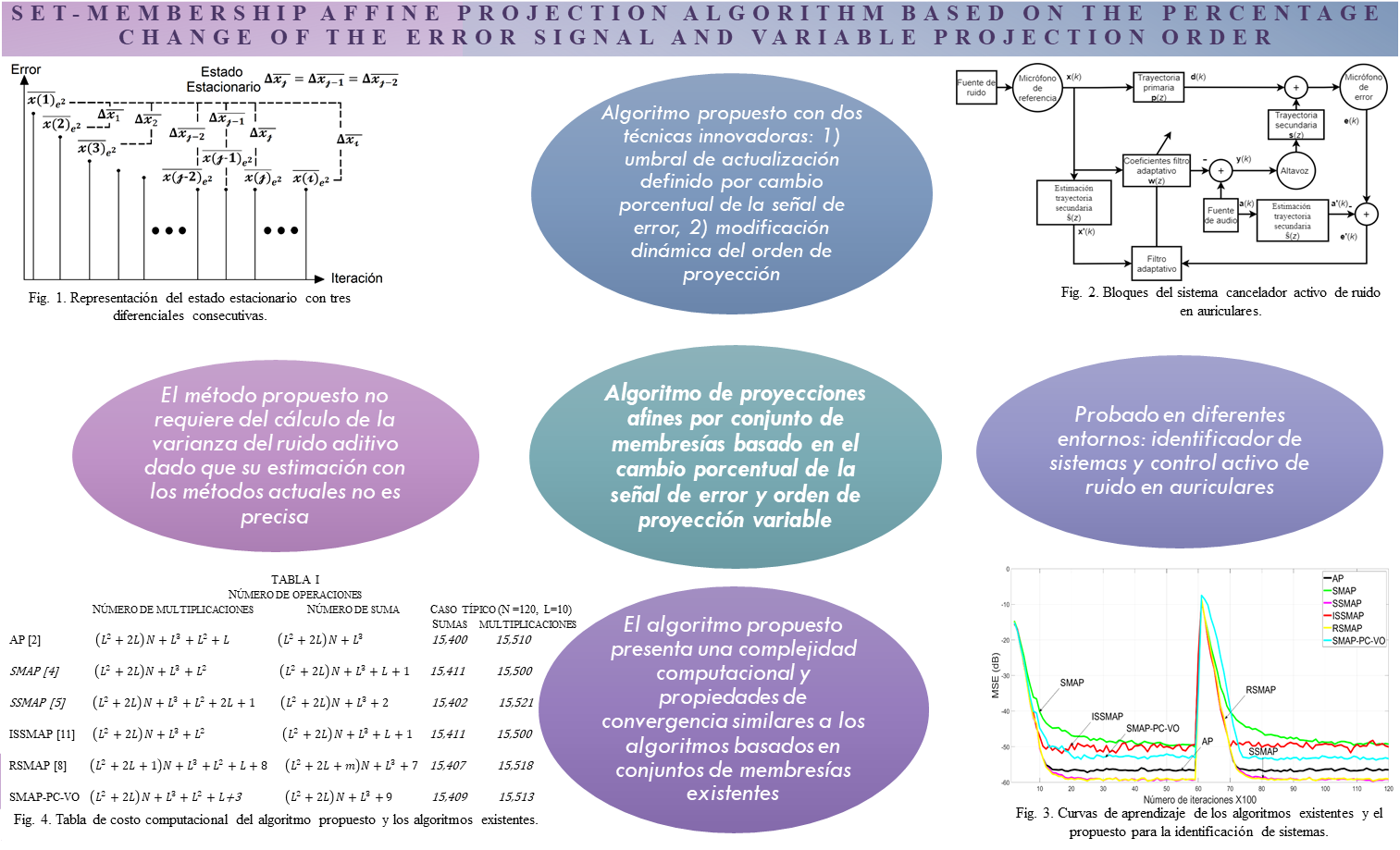
Nowadays, the use of adaptive filters plays an important role in multiple signal processing applications, such as active noise control, acoustic echo cancellers, system identifiers, channel equalizer, among others. Until date, many of the existing adaptive algorithms such as affine projection algorithms offer a high convergence speed. However, its computational cost is also high. Currently, several authors make extraordinary efforts to reduce its computational cost to be used in practical applications. In this paper, we propose a new set-membership affine projection algorithm based on the percentage change of the error signal and variable projection order (SMAP-PC-VO). Specifically, we propose two techniques to create this algorithm; 1) the new algorithm uses an error bound, which is obtained by calcuting the percentage change of the error signal, to avoid the computation of the variance of additive noise, since in existing approaches this parameter determines the error bound. In practical applications, the computation of the variance of additive noise is infeasible since this signal is not available; 2) we propose a new method to dynamically modify the projection order in the new algorithm. As a consequence, its computational cost is reduced. To demonstrate its performance, the proposed algorithm was successfully tested in different environments for system identification and active noise control for headphone applications. The simulation results demonstrate that the proposed algorithm presents good convergence properties. In addition, the proposed algorithm exhibits a low overall computational complexity.

Downloads

Download data is not yet available.

Author Biographies

Carlos Trejo, Instituto Politecnico Nacional

Carlos Alfonso Trejo received the M. in Educational Technology degree at DaVinci University, in 2013, the M. in Engineering in Computer Systems degree at Technological Institute of Higher Studies of Ecatepec, in 2019 and actually studies the Ph.D. degree in electronics and communications engineering from the National Polytechnic Institute, Mexico. He works on embedded systems and software engineering areas and recently he is interested on adaptive filtering tecniques.

Xochitl Maya, Instituto Politecnico Nacional

Xochitl Maya received the BS degree at Instituto Politécnico Nacional, Mexico, in 2017. Currently, she is a PhD student at the Instituto Politecnico Nacional, Mexico. Her research is focused on audio signal processing, active noise control and digital filtering.

Rene Martinez, Instituto Politecnico Nacional

René Martínez M.Sc. in microelectronics student at National Polytechnic Institute, Mexico, focused on the implementation in hardware of adaptive filters for noise cancelling applications.

Gabriel Sanchez, Instituto Politecnico Nacional

Gabriel Sánchez received the BS degree in Computer Science Engineering and the PhD degree in Electronic and Communications in 1999 and 2005, respectively, from the National Polytechnic Institute, Mexico City. He is a member of the National Researchers System of Mexico. His principal research interest is related to artificial neural networks.

Hector Perez, Instituto Politecnico Nacional

Hector Perez-Meana received the M.S. degree from the University of Electro-Communications, Tokyo Japan, a Ph. D. degree in Electrical Engineering from Tokyo Institute of Technology, Tokyo, Japan, in 1989. His principal research interests are adaptive systems, image processing, pattern recognition, information security and related fields. Dr. Perez-Meana is a member of the IEEE, IEICE, the National Researchers System of Mexico and the Mexican Academy of Science.

Juan Avalos, Instituto Politecnico Nacional

Juan-Gerardo Avalos was born in Mexico in 1984. He received the M.Sc. in microelectronics from the National Polytechnic Institute, Mexico, in 2010 and the Ph.D. degree in electronics and communications engineering from the National Polytechnic Institute, Mexico, in 2014. From 2011 to 2012 he was visiting researcher at the Vienna University of Technology, Austria. He is currently working as a Professor in the department of computer engineering, at the National Polytechnic Institute, Mexico

Giovanny Sanchez, Instituto Politecnico Nacional

Giovanny Sánchez received the M.S. degree at Instituto Politecnico Nacional, Mexico, in 2008, and the Ph.D. degree at Universitat Politecnica de Catalunya, Spain, in 2014. His research is focused on developing early auditory neural processing systems, neural-based cryptosystems in neuromorphic hardware, image and audio processing. Currently, he is an Associate Professor in the Instituto Politecnico Nacional, Mexico.

References

D. Trihinas, G. Pallis, y M. D. Dikaiakos, “Low-Cost Adaptive Monitoring Techniques for the Internet of Things”, IEEE Trans. Serv. Comput., vol. 14, núm. 2, pp. 487–501, mar. 2021, doi: 10.1109/TSC.2018.2808956.

K. Ozeki, Theory of Affine Projection Algorithms for Adaptive Filtering, vol. 22. Tokyo: Springer Japan, 2016. doi: 10.1007/978-4-431-55738-8.

J. R. Deller, “Set membership identification in digital signal processing,” IEEE ASSP Mag., vol. 6, no. 4, pp. 4–20, Oct. 1989, doi: 10.1109/53.41661

S. Werner y P. S. R. Diniz, “Set-membership affine projection algorithm”, IEEE Signal Process. Lett., vol. 8, núm. 8, pp. 231–235, ago. 2001, doi: 10.1109/97.935739.

P. S. R. Diniz, “Convergence Performance of the Simplified Set-Membership Affine Projection Algorithm”, Circuits Syst Signal Process, vol. 30, núm. 2, pp. 439–462, abr. 2011, doi: 10.1007/s00034-010-9219-z.

Md. Z. A. Bhotto y A. Antoniou, “Robust Set-Membership Affine-Projection Adaptive-Filtering Algorithm”, IEEE Trans. Signal Process., vol. 60, núm. 1, pp. 73–81, ene. 2012, doi: 10.1109/TSP.2011.2170980.

H. Zhao y Z. Zheng, “L 0 norm constraint set‐membership affine projection algorithm with coefficient vector reuse”, Electron. lett., vol. 52, núm. 7, pp. 560–562, abr. 2016, doi: 10.1049/el.2015.3386.

Z. Zheng y H. Zhao, “Robust Set-Membership Affine Projection Algorithm with Coefficient Vector Reuse”, Circuits Syst Signal Process, vol. 36, núm. 9, pp. 3843–3853, sep. 2017, doi: 10.1007/s00034-016-0471-8.

W. A. Martins, M. V. S. Lima, P. S. R. Diniz, y T. N. Ferreira, “Optimal constraint vectors for set-membership affine projection algorithms”, Signal Processing, vol. 134, pp. 285–294, may 2017, doi: 10.1016/j.sigpro.2016.11.025.

J. G. Avalos, J. Mendoza, F. A. Serrano, y G. Avalos, “Set-Membership Affine Projection-Like Algorithm with Evolving Order”, IEEE Latin Am. Trans., vol. 16, núm. 3, pp. 770–776, mar. 2018, doi: 10.1109/TLA.2018.8358654.

H. Yazdanpanah, P. S. R. Diniz, y M. V. S. Lima, “Improved simple set‐membership affine projection algorithm for sparse system modelling: Analysis and implementation”, IET signal process., vol. 14, núm. 2, pp. 81–88, abr. 2020, doi: 10.1049/iet-spr.2019.0294.

V. Belyi y W. Gan “A combined bilateral and binaural active noise control algorithm for closed-back headphones”, Applied Acoustics, p. 13, 2020.

Downloads

Published

2021-11-17

How to Cite

Trejo, C., Maya, X., Martinez, R., Sanchez, G., Perez, H., Avalos, J., & Sanchez, G. (2021). Set-membership affine projection algorithm based on the percentage change of the error signal and variable projection order. IEEE Latin America Transactions, 20(3), 496–502. Retrieved from https://latamt.ieeer9.org/index.php/transactions/article/view/5938

Issue

Vol. 20 No. 3 (2022): Ordinary Issue

Section

Articles