GPU-BRKGA: A GPU accelerated library for optimization using the biased random-key genetic algorithm
Keywords:
Genetic Algorithms, Optimization, GPU, MetaheuristicsAbstract
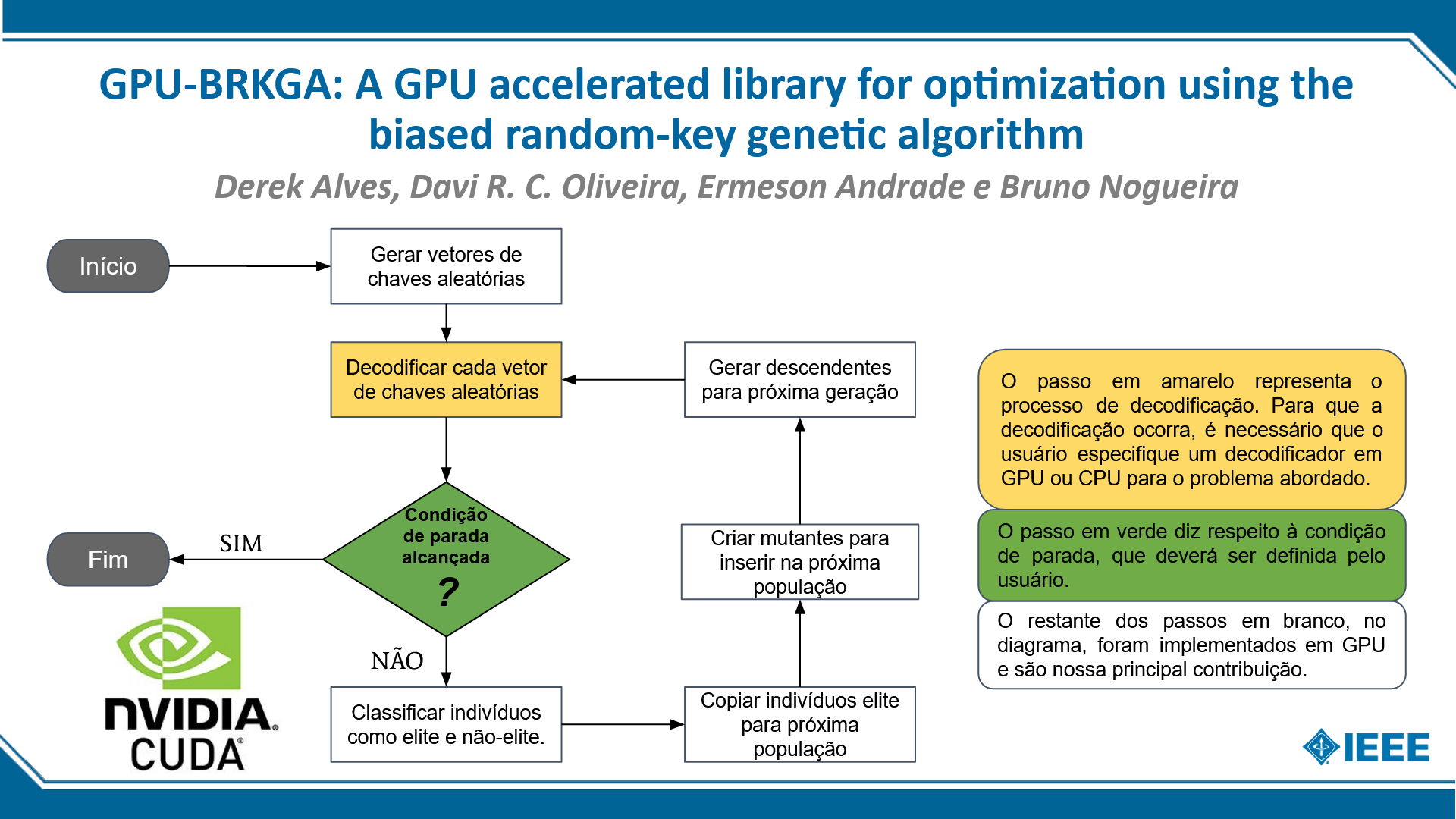
This paper presents a CUDA/C++ library, called GPU-BRKGA, for accelerating the biased random-key genetic algorithm (BRKGA). Our library features an easy to use API that allows designers with little experience in GPU development to accelerate the solution of their optimization problems. It automatically handles the problem-independent modules of BRKGA, and leaves the designer in charge with only the decoding procedure, that is, to convert a random-key vector into a solution to the optimization problem. We compared our solution with two other BRKGA API implementations: the standard CPU-based BRKGA API implementation (brkgaAPI) and another GPU-based BRKGA API from the literature (brkgaCuda). Experimental results show that GPU-BRKGA is up to 28x faster than brkgaAPI and up to 3x faster than brkgaCuda.
Downloads
References
B. Nogueira and R. G. Pinheiro, “A cpu-gpu local search heuristic for the maximum weight clique problem on massive graphs,”Computers &Operations Research, vol. 90, pp. 232–248, 2018.
B. Nogueira, E. Tavares, J. Araujo, and G. Callou, “Accelerating continuous grasp with a gpu,”The Journal of Supercomputing, vol. 75,no. 9, pp. 5741–5759, 2019.
B. Nogueira and R. G. Pinheiro, “A gpu based local search algorithm for the unweighted and weighted maximum s-plex problems,”Annals of Operations Research, vol. 284, no. 1, pp. 367–400, 2020.
B. Nogueira and E. Barboza, “A fpga-based accelerated architecture for the continuous grasp,”Computing, pp. 1–20, 2020.
F. Gonc ̧alves and M. G. Resende, “Biased random-key genetic algorithms for combinatorial optimization,”Journal of Heuristics, vol. 17,no. 5, pp. 487–525, 2011.
J. F. Gonc ̧alves, M. G. Resende, and J. J. Mendes, “A biased random-key genetic algorithm with forward-backward improvement for the resource constrained project scheduling problem,”Journal of Heuristics, vol. 17,no. 5, pp. 467–486, 2011.
M. G. Resende, “Biased random-key genetic algorithms with applications in telecommunications,”Top, vol. 20, no. 1, pp. 130–153, 2012.
A. Lima, R. Pinheiro, B. Nogueira, and R. Peixoto, “Algoritmo genético de chaves aleatórias viciadas para o problema do tempo de transmissão mínimo,” Oct 2020.
H. de Faria, M. G. Resende, and D. Ernst, “A biased random key genetic algorithm applied to the electric distribution network reconfiguration problem,”Journal of Heuristics, vol. 23, no. 6, pp. 533–550, 2017.
L. A. Roque, D. B. Fontes, and F. A. Fontes, “A biased randomkey genetic algorithm approach for unit commitment problem,”in International Symposium on Experimental Algorithms. Springer, 2011,pp. 327–339.
G. B. Mainieri, “Meta-heurística brkga aplicada a um problema de programação de tarefas no ambiente flowshop híbrido.” Ph.D. dissertation, Universidade de São Paulo, 2014.
S. M. Homayouni, D. B. Fontes, and F. A. Fontes, “A brkga for theintegrated scheduling problem in fmss,” in Proceedings of the Geneticand Evolutionary Computation Conference Companion, 2019, pp. 287–288.
F. T. Chan, R. Tibrewal, A. Prakash, and M. Tiwari, “Inventory based multi-item lot-sizing problem in uncertain environment: Brkga approach,” in Advances in Sustainable and Competitive ManufacturingSystems. Springer, 2013, pp. 1197–1206.
R. F. Toso and M. G. Resende, “A c++ application programming interface for biased random-key genetic algorithms,”Optimization Methods and Software, vol. 30, no. 1, pp. 81–93, 2015.
E. Xavier, “Uma interface de programac ̧ ̃ao de aplicac ̧ ̃oes para o brkgana plataforma cuda,” in Anais Principais do XX Simpósio em Sistemas Computacionais de Alto Desempenho. SBC, 2019, pp. 13–24.
J. C. Bean, “Genetic algorithms and random keys for sequencing and optimization,”ORSA journal on computing, vol. 6, no. 2, pp. 154–160,1994.[17] D. Merrill, “Nvidia cub,” https://nvlabs.github.io/cub/, 2020.
J. Momin and X.-S. Yang, “A literature survey of benchmark functions for global optimization problems,”Journal of Mathematical Modelling and Numerical Optimisation, vol. 4, no. 2, pp. 150–194, 2013.