Simplified SEP Approximations of Coherent Digital Modulation Schemes over \alpha-\kappa-\mu Fading Channel
Keywords:
wireless communication, approixmation theory, Gaussian Q function, symbol error rate, bit error rate, digital modulation schemes, multipath fading, $\alpha-\kappa-\mu$ fading, performance analysis and boundsAbstract
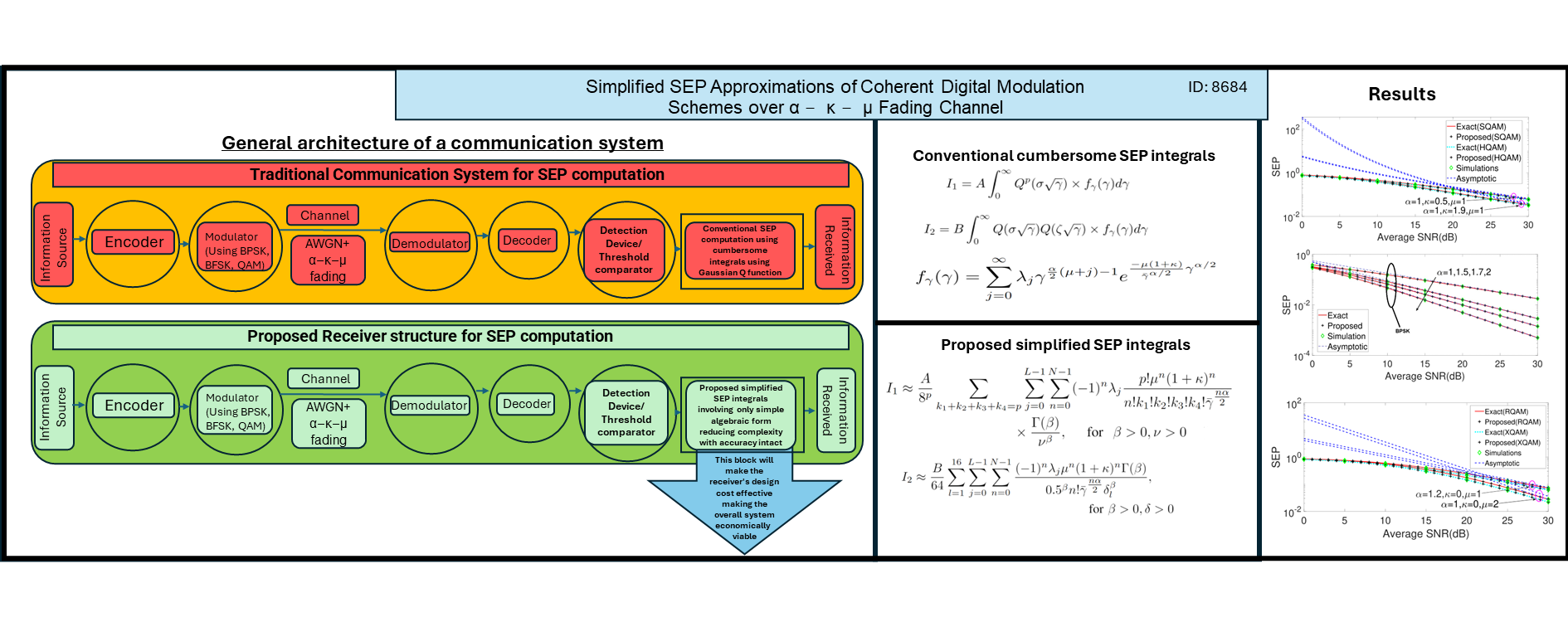
In this paper, we propose novel, simplified yet tight approximations of the error probability expressions of numerous digital modulation schemes over a popular \alpha-\kappa-\mu fading channel. With the help of a suitable approximation of the Gaussian Q-function and utilization of Taylor's series expansion, we facilitate the cumbersome integrals which play a key role in simplification of the performance evaluation metrics like symbol error probability (SEP) of various digital modulation schemes. This facilitates cost effective receiver's design making the overall system economically viable. We further illustrate the accuracy of the proposed SEP expressions with the help of the relative error. An insight on the truncation error (and its upper bound) is also highlighted in this paper. We also compute the relative error in the upper bound of the truncation error to further justify the accuracy of the proposed integrals. Moreover, the asymptotic expressions for the integrals are also provided which gives an idea regarding diversity order of the wireless communication systems for large signal to noise ratios.
Downloads
References
M. Ramirez and S. Molano, “Analytical expression for
the bit error rate of a filtered multitone modulation
scheme (FMT) through a multipath fading channel,”
IEEE Latin America Transactions, vol. 19, no. 4,
pp. 643–651, Apr. 2021. [Online]. Available: https:
//doi.org/10.1109/TLA.2021.9448547
A. Annamalai, C. Tellambura, and V. Bhargava, “A
general method for calculating error probabilities over
fading channels,” IEEE Transactions on Communica
tions, vol. 53, no. 5, pp. 841–852, May 2005. [Online].
Available: https://doi.org/10.1109/TCOMM.2005.847118
Y. M. Khattabi and S. A. Alkhawaldeh, “Performance
analysis of spatial modulation under rapidly time
varying Rayleigh fading channels,” IEEE Access,
vol. 7, pp. 110594–110604, 2019. [Online]. Available:
https://doi.org/10.1109/ACCESS.2019.2934000
M. K. Simon and M.-S. Alouini, Digital Communication
over Fading Channels, 2nd ed. Wiley, 2005. [Online].
Available: https://doi.org/10.1002/0471715220
M. D. Yacoub, “The α-µ distribution: A physical fading
model for the stacy distribution,” IEEE Transactions on
Vehicular Technology, vol. 56, no. 1, pp. 27–34, Jan.
[Online]. Available: https://doi.org/10.1109/TVT.
883753
M. Yacoub, “The κ − µ distribution and the η − µ
distribution,” IEEE Antennas and Propagation Magazine,
vol. 49, no. 1, pp. 68– 81, Feb. 2007. [Online]. Available:
https://doi.org/10.1109/MAP.2007.370983
M. Bilim, “Capacity and amount of fading analysis
for SIMO communications over η − µ and λ − µ
fading channels,” Digital Signal Processing, vol. 109,
p. 102921, 2021. [Online]. Available: https://doi.org/10.
/j.dsp.2020.102921
H. S. Silva, G. B. Lourenço, W. J. Queiroz, L. Aguayo,
I. E. Fonseca, and A. S. Oliveira, “On the performance
of digital systems in α − F fading and non-Gaussian
noise channels,” Digital Signal Processing, vol. 123,
p. 103445, 2022. [Online]. Available: https://doi.org/10.
/j.dsp.2022.103445
G. Fraidenraich and M. Yacoub, “The α − η −
µ and α−κ−µ fading distributions,” in IEEE
International Symposium on Spread Spectrum Techniques
and Applications, Aug. 2006, pp. 16– 20. [Online].
Available: https://doi.org/10.1109/ISSSTA.2006.311725
T. R. Rasethuntsa, M. Kaur, S. Kumar, P. S. Chauhan,
and K. Singh, “On the performance of DF-based
multi-hop system over α − κ − µ and α − κ − µ
extreme fading channels,” Digital Signal Processing,
vol. 109, p. 102909, 2021. [Online]. Available: https:
//doi.org/10.1016/j.dsp.2020.102909
S. Kumar, P. Chauhan, R. Bansal, M. Kaur, and
R. Yadav, “Performance analysis of CSS over α−η−µ
and α −κ−µ fading channel using clustering-based
technique,” Wireless Personal Communications, vol.
, 2022. [Online]. Available: https://doi.org/10.1007/
s11277-022-09880-y
S. Kalia, A. Joshi, and A. Agrawal, “Performance
analysis of spatial modulation over generalized α −
κ −µ fading distribution,” Physical Communication,
vol. 35, 2019. [Online]. Available: https://doi.org/10.
/j.phycom.2019.04.010
B. C. Le and S. Nguyen, “Evaluation of physical
layer security for UAV-enabled wireless networks
over α − κ−µ fading channels,” Wireless Personal
Communications, vol. 128, 2022. [Online]. Available:
https://doi.org/10.1007/s11277-022-10014-7
J. M. Moualeu, D. B. da Costa, W. Hamouda, U. S.
Dias, and R. A. de Souza, “Performance analysis
of digital communication systems over α-κ-µ fading
channels,” IEEE Communications Letters, vol. 23,
no. 1, pp. 192–195, Jan. 2019. [Online]. Available:
https://doi.org/10.1109/LCOMM.2018.2878218
A. Powari, G. Anand, and D. Sadhwani, “Novel range
wise optimization of the exponential bounds on the
Gaussian Q function and its applications in communica
tions theory,” IEEE Latin America Transactions, vol. 21,
no. 12, pp. 1237–1246, Dec. 2023. [Online]. Available:
https://doi.org/10.1109/TLA.2023.10305234
N. Kapucu, “On the performance of dual
branch selection diversity combining in α − κ − µ
fading environments,” Transactions on Emerging
Telecommunications Technologies, vol. 30, 2019.
[Online]. Available: https://doi.org/10.1002/ett.3719
E. Salahat and A. Hakam, “Performance analysis of
α-η-µ and α-κ-µ generalized mobile fading channels,”
in 20th European Wireless Conference, 2014. [Online].
Available: https://ieeexplore.ieee.org/document/6843156
J. M. Moualeu, D. B. da Costa, F. J. Lopez-Martinez, and
R. A. A. d. Souza, “On the performance of α– η– κ– µ
fading channels,” IEEE Communications Letters, vol. 23,
no. 6, pp. 967–970, Jun. 2019. [Online]. Available:
https://doi.org/10.1109/LCOMM.2019.2910526
A. Goswami and A. Kumar, “Performance analysis
of multi-hop wireless communication systems over
α −η −κ−µ channel,” Physical Communication,
vol. 33, 2018. [Online]. Available: https://doi.org/10.
/j.phycom.2018.12.004
I. S. Gradshteyn and I. M. Ryzhik, Table of Inte
grals, Series, and Products, 7th ed. New York: Aca
demic Press, 1980, https://www.sciencedirect.com/book/
/table-of-integrals-series-and-products.
D. Sadhwani, A. Powari, and N. Mehta, “New,
simple and accurate approximation for the Gaussian
Q function with applications,” IEEE Communications
Letters, vol. 26, no. 3, pp. 518–522, Mar. 2022.
[Online]. Available: https://doi.org/10.1109/LCOMM.
3135902
D. Sadhwani and R. Yadav, “A simplified exact
expression of SEP for cross QAM in AWGN channel
from MXNrectangular QAM and its usefulness in
Nakagami−m fading channel,” AEU- International
Journal of Electronics and Communications, vol. 74,
pp. 63–74, Apr. 2017. [Online]. Available: https:
//doi.org/10.1016/j.aeue.2017.01.014
L. Rugini, “Symbol error probability of hexagonal
QAM,” IEEE Communications Letters, vol. 20, no. 8,
pp. 1523–1526, Aug. 2016. [Online]. Available: https:
//doi.org/10.1109/LCOMM.2016.2574343
M. Simon, “Single integral representations of certain
integer powers of the Gaussian Q-function and their
application,” IEEE Communications Letters, vol. 6,
no. 12, pp. 532–534, Dec. 2002. [Online]. Available:
https://doi.org/10.1109/LCOMM.2002.806467
P. Vitthaladevuni, M.-S. Alouini, and J. Kieffer, “Exact
BER computation for cross QAM constellations,” IEEE
Transactions on Wireless Communications, vol. 4,
no. 6, pp. 3039–3050, Nov. 2005. [Online]. Available:
https://doi.org/10.1109/TWC.2005.857997
J. D. V. Sánchez, F. J. López-Martínez, J. F. Paris,
and J. M. Romero-Jerez, “The multi-cluster fluctuating
two-ray fading model,” IEEE Transactions on Wireless
Communications, pp. 1–1, 2023. [Online]. Available: