Convex Formulation for Optimal Active and Reactive Power Dispatch

Authors

Keywords:

Bilevel optimization, convex programming, opportunity costs, optimal power flow, strong duality

Abstract

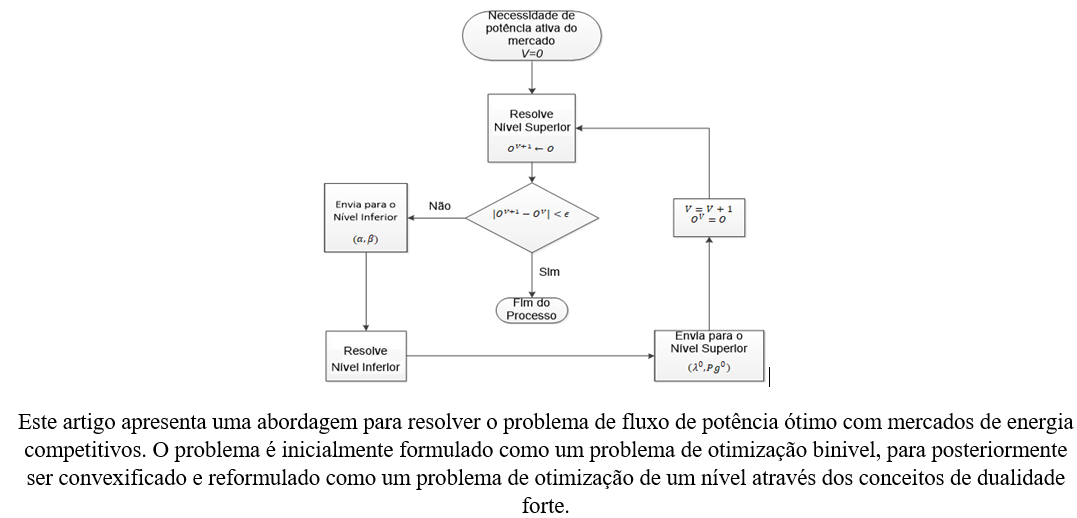
This paper proposes a convex programming model to solve the optimal power flow problem (OPF) related to the problems of generation active power dispatch and opportunity costs to meet the reactive power needs in energy markets. The problem is initially represented as a bilevel optimization problem where the upper level considers the minimization of opportunity costs of generating units through a second-order cone programming OPF model, and the lower level is a linear programming model that minimizes the value of active power offered by generators to the market energy. Subsequently, through the concept of strong duality, the problem is transformed into a one-level convex optimization model. Comparisons of the proposed modeling with other level formulations are presented. Results are presented for the IEEE14 and IEEE30 bus systems.

Downloads

Download data is not yet available.

Author Biographies

Mauro Viegas da Silva, Universidade do Estado de Mato Grosso

received the B.Sc. degree in Mathematics from the Mato Grosso Federal University in 1999, M.Sc. in Mathematics, and Ph.D. in electrical engineering from the São Paulo State University, Brazil, in 2011 and 2018, respectively. He is currently a professor at Mato Grosso Federal University. His research interests include the development of methodologies for the optimization, planning, and control, of electrical power systems.

Juan Manuel Home Ortiz, São Paulo State University – UNESP - Ilha Solteira, Brazil

received the B.Sc. and M.Sc. degrees in electrical engineering from the Universidad Tecnológica de Pereira, Colombia, in 2011 and 2014, respectively, and the Ph.D. degree in electrical engineering from the São Paulo State University (UNESP), Ilha Solteira, Brazil, in 2019. Currently, he is carrying out postdoctoral research with the UNESP. His research interests include the development of methodologies for the optimization, planning, and control, of electrical power systems.

Mahdi Pourakbari-Kasmaei, Aalto university

 (S’10–M’15–SM’19) received his Ph.D. degree in electrical engineering, power systems, from the Universidad Estadual Paulista (UNESP), Ilha Solteira, Brazil in 2015. He was a postdoctoral fellow at UNESP and also a visiting researcher at Universidad de Castilla-La Mancha, Spain, for about 15 months. He was a project executive of three practical projects, PI of three academic projects, and also a consultant in an electric power distribution company. Currently, he is with the Department of Electrical Engineering and Automation, Aalto University, Finland. He is also the Chairman of IEEE PES Finland IE13/PE31/34/PEL35 Joint Chapter. His research interests include power systems planning, operations, economics, and environmental issues.

José Roberto Sanches Mantovani, Department of Electrical Engineering, Power System Planning Lab, Sao Paulo State University (UNESP), Ilha Solteira–SP, Brazil

(M’06) received the B.Sc. degree from the Sao Paulo State University (UNESP), Ilha Solteira, Brazil, in 1981, and the M.Sc. and Ph.D. degrees from the University of Campinas, Campinas, Brazil, in 1987 and 1995, respectively, all in electrical engineering. He is currently a Professor with the Department of Electrical Engineering, UNESP. His research interests include the development of methodologies for the optimization, planning, and control of electrical power systems, and applications of artificial intelligence in power systems.

References

H. W. Dommel and W. Tinney, “Optimal power flow solutions,” IEEE Trans. Power Appar. Syst., vol. pas-87, no. 10, pp. 1866–1876, 1968.

D. I. Sun, B. Ashley, B. Brewer, A. Hughes, and W. F. Tinney, “Optimal power flow by newton approach,” IEEE Trans. Power Appar. Syst., vol. PAS-103, no. 10, pp. 2864–2880, 1984.

G. Torres; V.H. Quintana, "An interior-point method for non-linear optimal power flow using voltage rectangular coordinates", IEEE Trans. Power. Systems, New York, PWRS-13, n.4, p. 1211-1218, 1998

W.D. Rosehart, C.A. Cañizares and V.H. Quintana, V. H., “Multiobjective optimal power flow to evaluate voltage security costs in power networks;” IEEE Trans. Power Syst., vol. 18, N0. 2, pp.578-587, 2003.

L.L.Lai, J.T Ma, R. Yokoyama, M. Zhao, "Improved genetic algorithms for optimal power flow under both normal and contingent operation states", International Journal of Electrical Power & Energy Systems, Piscataway, v. 19, n. 5, p. 287-292, 1997.

G. Bakirtzis, P.N. Biskas, C.E. Zoumas, and V. Petridis, “Optimal power flow by enhanced genetic algorithm,” IEEE Transactions on Power Systems, vol. 17, 2002.

Abido, M. A., and N. A. Al-Ali. "Multi-objective differential evolution for optimal power flow." 2009 International Conference on Power Engineering, Energy and Electrical Drives. IEEE, 2009.

E. A. Amorim, S.H.M. Hashimoto, F.G.M. Lima, J.R.M. Mantovani, "Multi objective evolutionary algorithm applied to the optimal power flow problem", IEEE Latin America Transactions, V. 8, n. 3, p. 236-244, 2010.

J. R. S. Mantovani, S. a. G. Modesto, and a. V. Garcia, “VAr planning using genetic algorithm and linear programming,” IEE Proc. - Gener. Transm. Distrib., vol. 148, no. 3, p. 257, 2001.

J.M Home Ortiz, W,C. de Oliveira, J. R.S. Mantovani, "Optimal Power Flow Problem Solution Through a Matheuristic Approach", IEEE Access, V. 9, 2021.

J. Lavaei and S. H. Low, “Zero duality gap in optimal power flow problem,” IEEE Trans. Power Syst., vol. 27, no. 1, pp. 92–107, Feb. 2012.

D. K. Molzahn, J. T. Holzer, B. C. Lesieutre, and C. L. DeMarco, “Implementation of a large-scale optimal power flow solver based on semidefinite programming,” IEEE Trans. Power Syst., vol. 28, no. 4, pp. 3987–3998, 2013.

S. H. Low, “Convex relaxation of optimal power flow—Part I: Formulations and equivalence,” IEEE Trans. Control Netw. Syst., vol. 1, no. 1, pp. 15–27, Mar. 2014.

S. H. Low, “Convex relaxation of optimal power flow—Part II: Exactness,” IEEE Trans. Control Netw. Syst., vol. 1, no. 2, pp. 177–189, Jun. 2014.

X. Bai, H. Wei, K. Fujisawa, and Y. Wang, “Semidefinite programming for optimal power flow problems", Journal of Electric Power & Energy Systems, V. 30, No. 6, 2008.

A. J. Wood, B. F. Wollenberg, and G. B. Sheblé, Power generation, operation, and control. John Wiley & Sons, 2013.

F. D. Galiana, A. L. Motto, and F. Bouffard, “Reconciling social welfare, agent profits, and consumer payments in electricity pools,” IEEE Trans. Power Syst., vol. 18, no. 2, pp. 452–459, May 2003.

R. A. Jabr, “Optimal power flow using an extended conic quadratic formulation,” IEEE Trans. Power Syst., vol. 23, no. 3, pp. 1000–1008, Aug. 2008.

G. P. McCormick, “Computability of global solutions to factorable nonconvex programs: Part I—Convex underestimating problems,” Math. Program., vol. 10, pp. 147--175, 1976.

P. M. Castro, “Tightening piecewise McCormick relaxations for bilinear problems,” Comput. Chem. Eng., vol. 72, pp. 300–311, Jan. 2015.

B. Colson, P. Marcotte, and G. Savard, “An overview of bilevel optimization,” Ann. Oper. Res., vol. 153, no. 1, pp. 235–256, Sep. 2007.

V. V. Kalashnikov, S. Dempe, G. A. Pérez-Valdés, N. I. Kalashnykova, and J.-F. Camacho-Vallejo, “Bilevel programming and applications,” Math. Probl. Eng., vol. 2015, pp. 1–16, 2015.

W.A. BUKHSH, A. Grothey, K.I.M. McKinnon, P.A. Troden, "Local solutions of the optimal power flow problem" IEEE Transactions on Power Systems, Piscataway, v. 28, n. 4, p. 4780-4788, 2013.

Artelys, “Knitro.” [Online]. Available: https://www.artelys.com/solvers/knitro/.

O. Alsac and B. Stott, “Optimal Load Flow with Steady-State Security,” IEEE Trans. Power Appar. Syst., vol. PAS-93, no. 3, pp. 745–751, May 1974.

[Online]. Available: https://drive.google.com/drive/folders/10trw5olLl31GhQNYwW63a5QFp9ic5Daz?usp=sharing.

Downloads

Published

2022-01-07

How to Cite

Viegas da Silva, M., Home Ortiz, J. M., Pourakbari-Kasmaei, M., & Sanches Mantovani, J. R. (2022). Convex Formulation for Optimal Active and Reactive Power Dispatch. IEEE Latin America Transactions, 20(5), 787–798. Retrieved from https://latamt.ieeer9.org/index.php/transactions/article/view/6031

Issue

Vol. 20 No. 5 (2022): Ordinary Issue

Section

Articles

Most read articles by the same author(s)