A Novel Hybrid (PID + MRAC) Adaptive Controller for an Air Levitation System
Keywords:
adaptive controller, air levitation system, HMRAC, Lyapunov functionAbstract
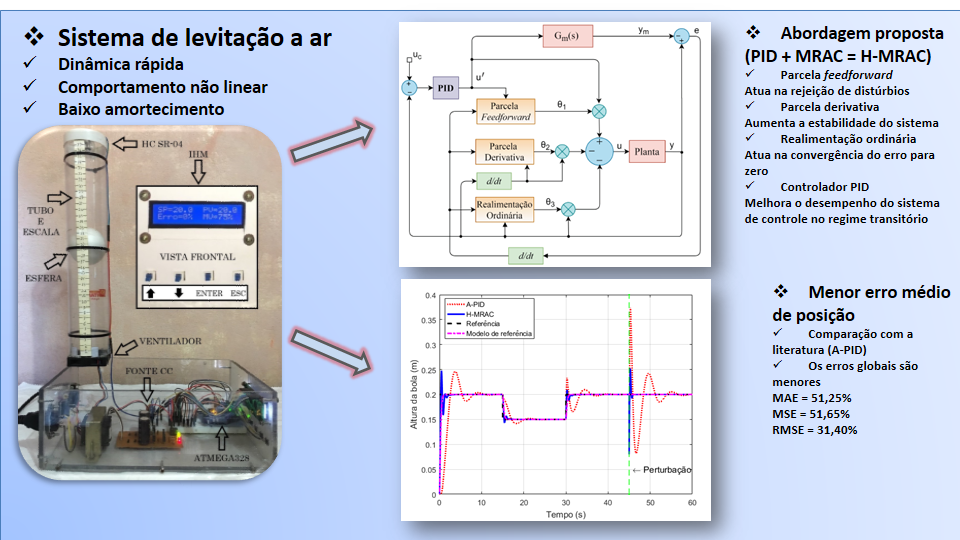
The air levitation system belongs to a class of systems with fast dynamics and low damping. Such characteristics make the plant intrinsically unstable and respond in a non-linear form. Thus, it is prohibitive to use classic control techniques, such as the PID (Proportional-Integral-Derivative) controller, to track the position of the sphere. The control system must be able to compensate the non-linearities, high oscillation and reject disturbances. Thus, this research proposes to create a new approach for the hybrid controller (PID + MRAC) present in the literature. The topological character of the proposed MRAC (Model Reference Adaptive Controller) consists of three parts: a feedforward controller, a derivative portion and an ordinary feedback. The feedforward portion has the purpose of rejecting undesirable disturbances. The derivative portion increases the stability of the system and the ordinary feedback makes the error null in steady state. Due to the convergence time of the adjustment parameters, MRAC performs poorly during reference changes and in the rejection of disturbances. Thus, it is common practice to use the MRAC with the PID controller. In its methodological aspect, the control law was created from Lyapunov's theory, with the purpose of ensuring asymptotic stability for the system. As a result, the proposed controller (Hybrid-MRAC or H-MRAC) showed better results than a literature reference (A-PID), in terms of mean absolute (MAE), mean square (MSE) and root mean square (RMSE) errors. In MAE simulations it was 51,25% lower on average, MSE was 51,65% and RMSE 31,40%. In the experiments, the MAE was on average 19,72% lower, the MSE 42,92% and the RMSE 18,58%.
Downloads
References
M. A. Andrade, F. Buiochi, and J. C. Adamowski, “Finite element
analysis and optimization of a single-axis acoustic levitator,” IEEE transactions
on ultrasonics, ferroelectrics, and frequency control, vol. 57,
no. 2, pp. 469–479, 2010.
D. Ilssar, I. Bucher, and H. Flashner, “Modeling and closed loop control
of near-field acoustically levitated objects,” Mechanical Systems and
Signal Processing, vol. 85, pp. 367–381, 2017.
M. A. Andrade, N. Perez, F. Buiochi, and J. C. Adamowski, “Matrix
method for acoustic levitation simulation,” IEEE transactions on ultrasonics,
ferroelectrics, and frequency control, vol. 58, no. 8, pp. 1674–1683,
P. A. Q. Assis and R. K. H. Galvao, “Sliding mode predictive control of
a magnetic levitation system employing multi-parametric programming,”
IEEE Latin America Transactions, vol. 15, no. 2, pp. 239–248, 2017.
B. Singh and V. Kumar, “A real time application of model reference
adaptive pid controller for magnetic levitation system,” in
IEEE Power, Communication and Information Technology Conference
(PCITC). IEEE, 2015, pp. 583–588.
L. H. Torres, L. Schnitman, C. Junior, and J. F. de Souza, “Feedback
linearization and model reference adaptive control of a magnetic levitation
system,” Studies in Informatics and Control, vol. 21, no. 1, pp.
–74, 2012.
L. E. Venghi, G. N. Gonzalez, and F. M. Serra, “Implementation
and control of a magnetic levitation system,” IEEE Latin America
Transactions, vol. 14, no. 6, pp. 2651–2656, 2016.
J. Zhang, X. Wang, and X. Shao, “Design and real-time implementation
of takagi–sugeno fuzzy controller for magnetic levitation ball system,”
IEEE Access, vol. 8, pp. 38 221–38 228, 2020.
C. Caro and N. Quijano, “Low cost experiment for control systems,” in
IX Latin American Robotics Symposium and IEEE Colombian Conference
on Automatic Control,. IEEE, 2011, pp. 1–6.
J. Chac´on, H. Vargas, S. Dormido, and J. S´anchez, “Experimental
study of nonlinear pid controllers in an air levitation system,” IFACPapersOnLine,
vol. 51, no. 4, pp. 304–309, 2018.
D. Chaos, J. Chacon, E. Aranda-Escol´astico, and S. Dormido, “Robust
switched control of an air levitation system with minimum sensing,” ISA
transactions, vol. 96, pp. 327–336, 2020.
E. Chołodowicz and P. Orłowski, “Low-cost air levitation laboratory
stand using matlab/simulink and arduino,” Pomiary Automatyka Robotyka,
vol. 21, 2017.
L. dos Santos Coelho and M. W. Pessˆoa, “Nonlinear model identification
of an experimental ball-and-tube system using a genetic programming
approach,” Mechanical Systems and Signal Processing, vol. 23, no. 5,
pp. 1434–1446, 2009.
L. Herrmann and M. Broecker, “Flatness based control of a ball in tube
system,” IFAC-PapersOnLine, vol. 48, no. 1, pp. 790–795, 2015.
G. Liauˇcius, V. Kaminskas, and R. Liutkeviˇcius, “Digital self-tuning
pid control of pressure plant with closed-loop optimization. information
technology and control,” Information Technology and Control, vol. 40,
no. 3, pp. 202–209, 2011.
G. Liauˇcius, V. Kaminskas, T. Krilaviˇcius, A. L. Telksnys, J. Augutis,
G. Dzemyda, H. Praneviˇcius, E. K. Zavadskas, G. Raˇskinis, and
R. ˇ Seinauskas, “Digital self-tuning control of pressure plant,” Tese de
doutorado, Vytauto Didˇziojo universitetas, 2014.
R. Masoudi, S. Yousefizadeh, P. Hajiani, and J. Zarei, “Position control
of two balls in two interconnected vertical tubes using controlled dc fans
and sliding mode control,” in International Conference on Mechatronics
and Control (ICMC). IEEE, 2014, pp. 1629–1633.
O. Ziwei, S. Michael, andW. Kexin, “The experiment “ball-in-tube” with
fuzzy-pid controller based on dspace,” in IEEE International Conference
on Systems, Man and Cybernetics. IEEE, 2007, pp. 877–881.
R. C. Dorf and R. H. Bishop, Modern control systems. Pearson, 2011.
N. J. Nilsson, Principles of artificial intelligence. Morgan Kaufmann,
G. Liauˇcius and V. Kaminskas, “The independent fuzzy control with
correction of two dimensional process,” in Electrical and control technologies:
proceedings of the 4th international conference on electrical
and control technologies, Kaunas, Lithuania. Kaunas: Technologija, 4,
D. Zhang and B. Wei, “Design, analysis and modelling of a hybrid
controller for serial robotic manipulators,” Robotica, vol. 35, no. 9, pp.
–1905, 2017.
L. E. G. Castanon, A. V. Martinez, and R. C. Reynoso, “Mrac-based
fault tolerant control of a siso real process application,” IEEE Latin
America Transactions, vol. 13, no. 8, pp. 2545–2550, 2015.
K. J. A° stro¨m and B. Wittenmark, “Adaptive control. mineola,” 2008.
H. K. Khalil and J. W. Grizzle, Nonlinear systems. Prentice hall Upper
Saddle River, NJ, 2002, vol. 3.
M. Vidyasagar, Nonlinear systems analysis. SIAM, 2002.
L. A. Aguirre, Introduc¸ ˜ao `a identificac¸ ˜ao de sistemas: t´ecnicas lineares
e n˜ao lineares aplicadas a sistemas reais. Editora da UFMG. 3ª edic¸ ˜ao,
V. H. Haendel, A. B. Fontes, J. S. Lima, and M. O. Sobrinho, “T´ecnicas
de identificac¸ ˜ao em malha fechada usando o algoritmo vari´avel instrumental:
Um estudo de caso,” in Simp´osio Brasileiro de Automac¸ ˜ao
Inteligente - SBAI, 2013.
S. Kay, Intuitive probability and random processes using MATLAB®.
Springer Science & Business Media, 2006.
M. M. Mukaka, “A guide to appropriate use of correlation coefficient in
medical research,” Malawi medical journal, vol. 24, no. 3, pp. 69–71,
R. Pal, Predictive modeling of drug sensitivity. Academic Press, 2016.