Linear Algebra Based Control: Application to a second order chained form system
Keywords:
non-holonomic system, linear algebra, nonlienar tracking control, positioningAbstract
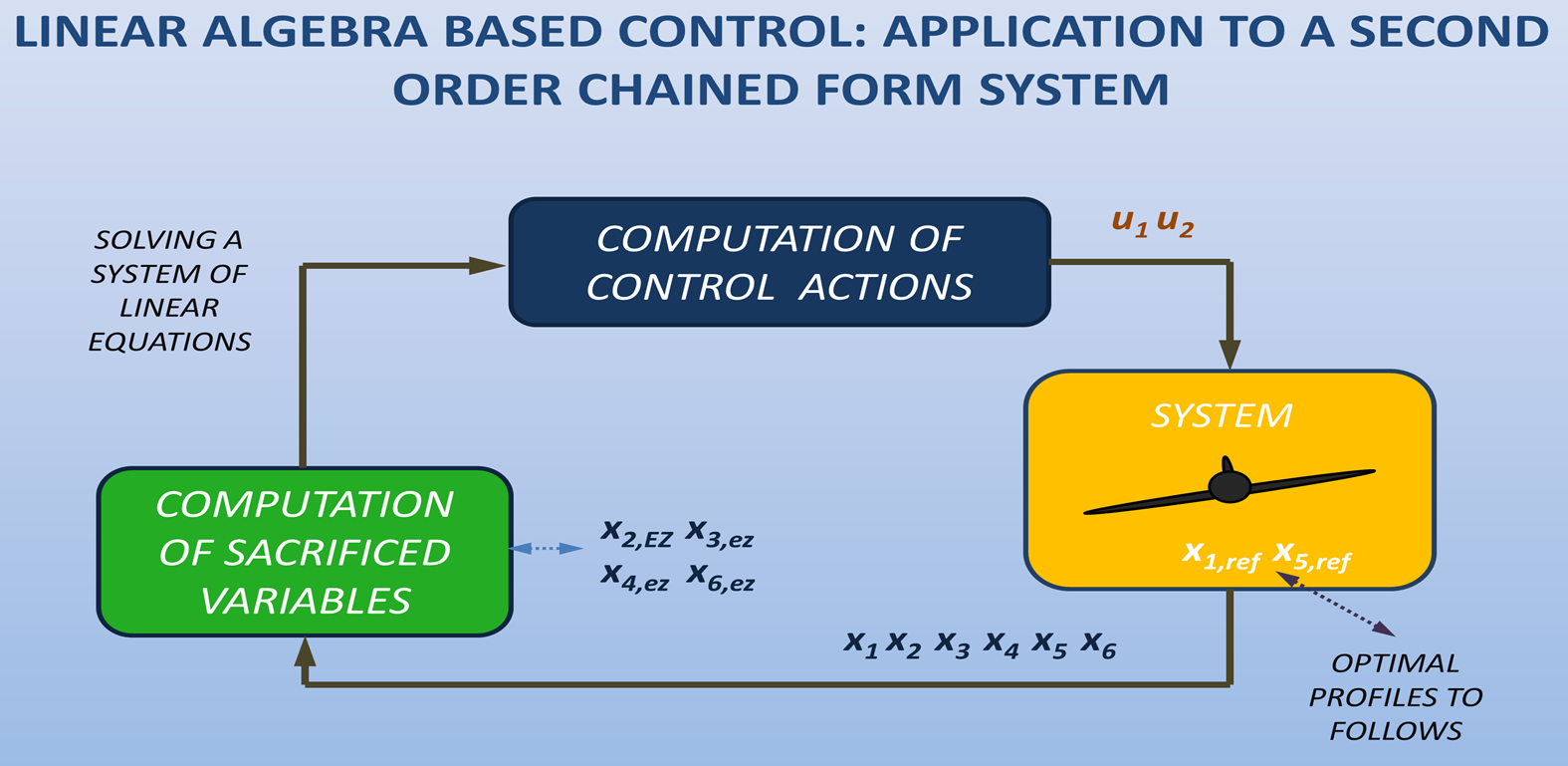
Control of underactuated systems with non-holonomic constraints has been an issue of interest in recent years. These systems are hard to control because their linearization makes them uncontrollable and current approaches generally involve complex calculations. In this manuscript, a controller for trajectory tracking and positioning for a second-order chained form system using a simple approach based on linear algebra is proposed. The control law is formulated by setting two of the six variables trajectories, while the other four are calculated assuming the equations system has an exact solution, and ensuring the error tends to zero. The stability of the proposed control system is demonstrated through the Khalil Lemma, and simulations show the performance of the controller.
Downloads
References
N. P. I. Aneke, “Control of underactuated mechanical systems,” PhD dissertation, Department of Mechanical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands, 2003.
R.W. Brockett, R.S. Millman, H.J. Sussmann, “Asymptotic stability and feedback stabilization,” in Differential Geometric Control Theory, Eds. pp. 2961–2963, 1983.
N. P. Aneke, H. Nijmeijer, A.G. de Jager, “Tracking control of second-order chained form systems by cascaded backstepping” International Journal of Robust and Nonlinear Control, vol. 13, pp. 95-115, 2003.
Y. P. Tian and K. C. Cao, “Time-varying linear controllers for exponential tracking of nonholonomic systems in chained form,” International Journal of Robust and Nonlinear Control, vol. 17, pp. 631–647, 2007.
Z. P. Yuan, Z. P. Wang and Q. J. Chen, "Trajectory tracking control of a nonholonomic mobile robot," IEEE ICCA 2010, Xiamen, pp. 2207-2211, 2010.
M. Asif, M. J. Khan, N. Cai, “Adaptive sliding mode dynamic controller with integrator in the loop for nonholonomic wheeled mobile robot trajectory tracking,” International Journal of Control, vol. 87, pp 964-975, 2014.
M.A. Fairus, Z. Mohamed, M.N. Ahmad, W.S. Loi “LMI-based multi objective integral sliding mode control for rotary inverted pendulum system under load variations,” Journal Teknologi. vol. 73, pp. 125-137, 2015.
M. Sarfraz, “Stabilization of Perturbed Nonholonomic Systems in Chained Form”. Ph.D. Thesis, Capital University of Science and Technology, Islamabad, Pakistan, 2018.
G. He, C. Zhang, W. Sun, Z. Geng, “Stabilizing the second-order nonholonomic systems with chained form by finite-time stabilizing controllers,” Robotica, vol. 34, pp. 2344-2367, 2016.
M. Ito, “Motion Planning of a Second-Order Nonholonomic Chained Form System Based on Holonomy Extraction”. Electronics, 8, 1337, 2019.
..H. Arai, K. Tanie, N. Shiroma, “Nonholonomic control of a three-DOF planar underactuated manipulator”. IEEE Trans. Robot. Autom. 14, 681–695. 1998.
...I. Fantoni, R. Lozano, “Non-Linear Control for Underactuated Mechanical Systems”. Springer-Verlag, 2002
D. Gandolfo, C. Rosales, , D. Patiño, , G. Scaglia, and M. Jordan, “Trajectory Tracking Control of a PVTOL Aircraft Based on Linear Algebra Theory”. Asian J Control, 16: 1849-1858, 2014.
Scaglia Serrano Mario Emanuel, Albertos Pedro (2020). “Linear Algebra Based Controller - Design and Applications”. Publisher: Springer International Publishing. [15] G. Scaglia, E. Serrano, A. Rosales, and P. Albertos, “Tracking Control Design in Nonlinear Multivariable Systems: Robotic Applications”, Mathematical Problems in Engineering, vol. 2019, Article ID 8643515, 15 pages, 2019.
M. E. Serrano, D. C. Gandolfo, G. J.E. Scaglia, “Trajectory tracking controller for unmanned helicopter under environmental disturbances”, ISA Transactions, 2020.
M.C. Fernández, M.N. Pantano, S. Rómoli, D. Patiño, O.A. Ortiz, G.J.E. Scaglia, "An Algebra Approach for Nonlinear Multivariable Fed-Batch Bioprocess Control". International Journal of Industrial and Systems Engineering, 2019.
L. Guevara, O. Camacho, A. Rosales, J. Guevara, G. Scaglia. “A linear algebra controller based on reduced order models applied to trajectory tracking for mobile robots: an experimental validation”. Int. J. Automation and Control, 13, 2, 2019. [19] H.K. Khalil, “Nonlinear Systems,” Second Edition. Prentice-Hall. New Jersey. United States of America, 1996.
M. C. F. Puchol, M. N. Pantano, S. Godoy, E. Serrano, G. Scaglia. Optimización de Parámetros Utilizando los Métodos de Monte Carlo y Algoritmos Evolutivos. Aplicación a un Controlador de Seguimiento de Trayectoria en Sistemas no Lineales. Revista Iberoamericana de Automática e Informática industrial. v. 16, n. 1, p. 89 99, 2019.
María N. Pantano, María C. Fernández, Mario E. Serrano, Oscar A. Ortiz, and Gustavo J. E. Scaglia. “Tracking Control of Optimal Profiles in a Nonlinear Fed-Batch Bioprocess under Parametric Uncertainty and Process Disturbances” Ind. Eng. Chem. Res. 2018, 57, 32, 11130-11140.
E. Serrano, Daniel C. Gandolfo, Francisco Rossomando, Gustavo J.E. Scaglia. “Estimation based controller for marine vessel exposed to environmental perturbations”, Ocean Engineering, 2019, 187, 106199.