Comparative Analysis of Different Preconditioning Methods in Electromagnetic Scattering Problems using MoM-FMM
Keywords:
EFIE MoM FMM iLU SPAI GMRES RCSVVAbstract
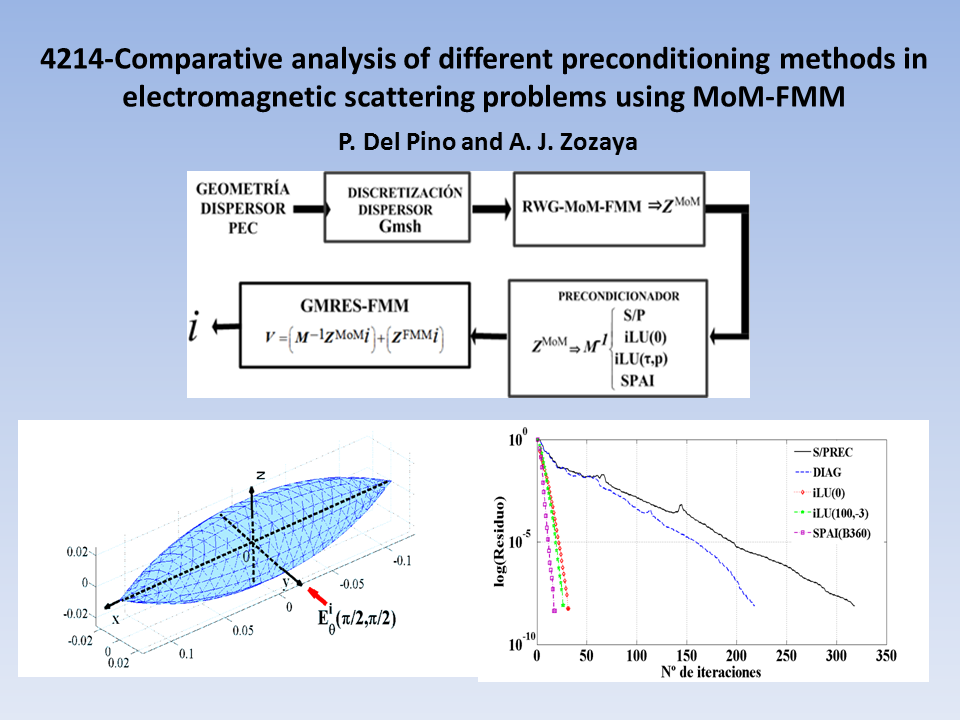
The numerical solution of the electric field integral equation in electromagnetic scattering problems involving metallic bodies, using the method of moments in conjunction with the fast multipole method, gives rise a full matrix with highly spread complex eigenvalues and consequently with a low condition number. Thus, iterative methods may not converge or it will require an extremely large number of iterations, which make this strategy unfeasible due to the high solution time and the expensive computational resources required. To overcome this drawback, the system matrix must be preconditioned to ensure the convergence in a reasonable number of iterations and with appropriate accuracy. In this work, some preconditioning techniques are revised and applied to a linear equation system derived from such type of problems, and the performance of these preconditioners is estimated and analyzed comparatively using the generalized minimal residual iterative method.
Downloads
References
R. F. Harrington. “Time Harmonic Electromagnetics Fields”. McGraw Hill, 1961.
C.A. Balanis. “Advanced Engineering Electromagnetics.” John Wiley & Sons, New York, 1989.
J. Markkanen, P. Ylä-Oijala, A. Sihvola, “Discretization of volume integral equation formulations for extremely anisotropic materials,” IEEE Transactions on. Antennas and Propagation..vol. 60, no. 11, pp. 5195-5202, Nov. 2012.
H. Feshbach and P. Morse. “Methods of Theoretical Physics. Part I”. 1953.
R. F. Harrington. “Field Computation by Moment Methods”. IEEE Press Series on Electromagnetic Waves, 1993.
E. Arvas and L. Sevgi. “A Tutorial on the Method of Moments” IEEE Antennas and Propagation Magazine, Vol. 54, No. 3, June 2012.
W. C: Gibbson. “The Method of Moments in Electromagnetics”. Chapman & Hall/CRC, 2008.
A. W. Glisson S. M. Rao, D. R. Wilton. “Electromagnetic scattering by surfaces of arbitrary shape”. IEEE Transactions on Antennas and Propagation, AP-30: pp. 409–418, 1982.
B. A. Cipra. “The best of the 20th century: Editors name top 10 algorithms”. SIAM News, 33, Number 4.
E. Michielssen J.M. Song W.C. Chew, J.M. Jin. “Fast and efficient algorithms in computational electromagnetic”. Norwood, MA, 2001.
A. T. Ihler. “An overview of fast multipole methods”. April 23, 2004.
V. Rokhlin y S.Wandzura R. Coifman. “The fast multipole method for the wave ecuation: a pedestian prescription”. IEEE Antennas and Propagation Magazine, 35 no. 3, June 1993.
V. Rokhlin L. Greengard. “A fast algorithm for particle simulation”. Journal of Computational Physics, 43: pp. 325–348, 1987.
W. C. Chew J. M. Song. “Error analysis for the truncation of multipole expansión of vector green’s functions”. IEEE Microwave Wireless Components Letters, 11 no. 7: pp. 311–313, 2001.
A. Zozaya and Paulino Del Pino. “A simple numerical experiment of Green’s function expansión in the Fast Multipole Method”. Adavanced Electromagnetics, vol 6, no. 4, November 2017.
Y. Saad. “Iterative Methods for Sparse Linear Systems”. Pws Publishing Company, Boston, 1996.
M. Versaci & et al. “Krylov’s subspaces iterative methods to evaluate electrostatic parameters” American Journal of Applied Sciences, 11 (3): 396-405, 2014. doi:10.3844/ajassp.2014.396.
R. Barret & et al. “Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods”. SIAM, http://www.siam.org/books. Philadelphia, 1994.
Henk A. van der Vorst. “Iterative Methods for Large Linear Systems”. Mathematical Institute Utrecht University Utrecht, The Netherlands, 2002.
Jan Brandts. “Projection methods for oversized linear algebra problems”. Mathematisch Instituut, Universiteit Utrecht, NAW 5/1:264–276, 2000.
KE CHEN. “Matrix Preconditioning Techniques and Applications”. Cambridge University Press, volume 19. 2005.
Michele Benzi. “Preconditioning techniques for large linear systems: A survey”. Journal of Computational Physics, 182:418–477, 2002.
X.-Min Pan and X.-Qing Sheng. “Improved Algebraic Preconditioning for MoM Solutions of Large-Scale Electromagnetic Problems”. IEEE Antennas and Wireless Propagation Letters, vol. 13, 2014. doi: 10.1109/LAWP.2013.2295239.
O. Wiedenmann and T. F. Eibert. “The effect of near-zone preconditioning on electromagnetic integral equations of first and second kind”. Adv. Radio Sci., 11, 61–65, 2013. doi 10.5194/ars-11-61-2013.
H. Anzt, E. Chow, J. Saak and J. Dongarra. “Updating incomplete factorization preconditioners for model order reduction”. Numerical Algorithms. 73 (3), pp. 611–630. Springer Science+Business Media New York . 2016 doi 10.1007/s11075-016-0110-2.
T. Malas, T. and L. Gurel. “Incomplete LU preconditioning with Multilevel Fast Multipole Algorithm for electromagnetic scattering”. SIAM J. Scientific Computing, vol. 29, no. 4, pp. 1476 -1494, 2007.
Y. Saad. Ilut: “A dual threshold incomplete LU factorizations”. SIAM Numerical Linear Algebra with Applications, 1994.
Y. Saad E. Chow.”Approximate inverse preconditioners via sparse sparse iterations”. SIAM Journal on Scientific Computing, 19-3: pp. 995–1023, 1994.
C. K. Papadopoulos∗and Gavvanis “Generic Approximate Sparse Inverse Matrix Techniques”. International Journal of Computational Methods. Vol. 11, No. 6 (2014). DOI: 10.1142/S0219876213500849.
D. Bertaccini and S. Filippone. “Sparse approximate inverse preconditioners on high performance GPU platforms”. Computers and Mathematics with Applications 71 (2016) 693–711. DOI: 10.1016/j.camwa.2015.12.008.
Christophe Geuzaine and Jean-François Remacle. “A three dimensional finite element mesh generator with built-in pre- and post-processing facilities”. International Journal for Numerical Methods in Engineering 79(11), pp. 1309-1331, 2009. https://gmsh.info/doc/texinfo/gmsh.html