Neural Control for Epidemic Model of Covid-19 with a Complex Network Approach

Authors

Keywords:

Neural Network, COVID-19, complex network

Abstract

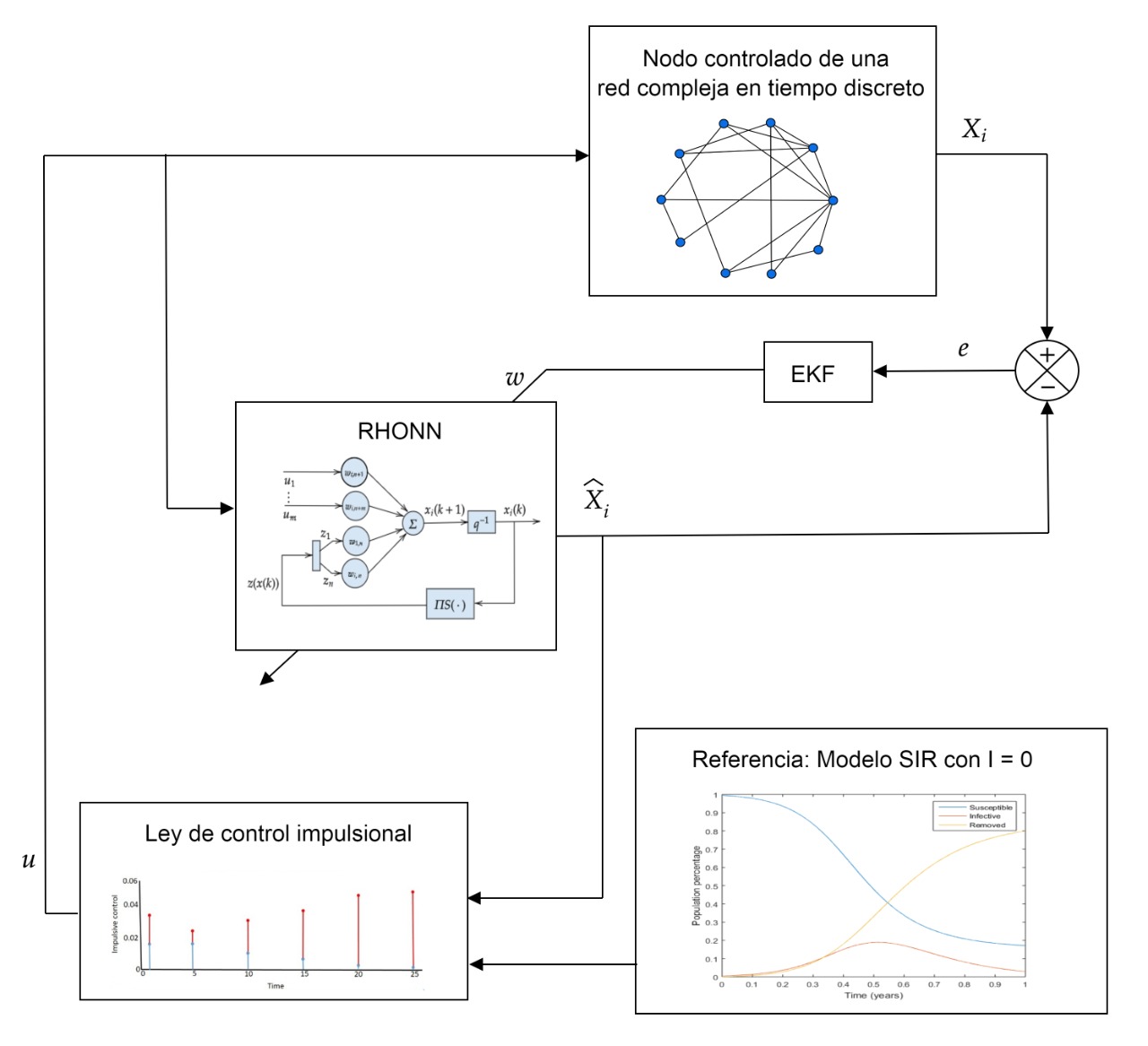
This paper presents the mathematical model Susceptible-Infected-Recovered SIR with parameters that describe the COVID-19 dynamics. This model is based on a system of ordinary differential equations in which appropriate conditions and starting parameter values such as transmission rates and recovery rates are considered known. These parameters are utilized to obtain a simulation of COVID-19 behavior, in order to establish a possible solution to avoid a greater chance of disease transmission. On the proposed scheme, we use a neural impulsive inverse optimal control for a complex network in which the dynamic of each node is a discrete version of SIR model that describe the dynamics of COVID-19. The neural network is trained with an extended Kalman’s filter and is used as a neural identifier for the selected nodes of the system. The control law used represents a hypothetical treatment for COVID-19. This work aims to simulate the interaction of different populations during an epidemic outbreak in which populations are represented by the complex network nodes

Downloads

Download data is not yet available.

Author Biographies

Alma Y. Alanis, University of Guadalajara

Alma Y. Alanis, (SM’04, M’08, S’14) received the M.Sc. and Ph.D. degrees in electrical engineering from the Advanced Studies and Research Center of the National Polytechnic Institute, Centro de Investigacion y de Estudios Avanzados del IPN, Guadalajara, Mexico, in 2004 and 2007, respectively. Since 2008, she has been with the University of Guadalajara, Guadalajara, where she is currently the Chair Professor with the Department of Computer Science. She is also a member of the Mexican National Research System (SNI-2) and member of the Mexican Academy of Sciences. Her research interest centers on neural control, backstepping control, block control, and their applications to electrical machines, power systems, biomedical systems and robotics

Esteban A. Hernandez-Vargas, Universidad Nacional Autónoma de Mexico

Esteban A. Hernandez-Vargas (M’08) received the Ph.D. degree in mathematics from the Hamilton Institute, National University of Ireland, Galway, Ireland, in 2011. For three years, he held a post-doctoral scientist position at the Helmholtz Centre for Infection Research (HZI), Braunschweig, Germany, where he founded the pioneering Research Group of Systems Medicine of Infectious Diseases in 2014. Since 2017, he and his research group moved to the Frankfurt Institute for Advanced Studies, Frankfurt, Germany.

Nancy F. Ramirez, University of Guadalajara

Nancy F. Ramírez received her bachelor of Informatics in 2006 from Tecnológico Nacional de México. Since 2008 she has worked for Universidad de Guadalajara CU Costa Sur. In 2013 she obtained a Master’s degree in Computational Engineering from the Universidad de Guadalajara and where she currently holds a Ph. D. in Electronics and Computing. The research areas where she developed are epidemiological models and complex networks.

Daniel Rios-Rivera, University of Guadalajara

Daniel Ríos-Rivera received his bachelor degree in Mechatronic Engineering from Tecnológico Nacional de México in 2015, and his M.Sc. in Electronic Engineering and Computing from Universidad de Guadalajara where he is currently doing his Ph.D. in Electronics and Computing. His main research interest are automatic control and complex networks.

Downloads

Published

2021-06-08

How to Cite

Alanis, A. Y., Hernandez-Vargas, E. A., Ramirez, N. F., & Rios-Rivera, D. (2021). Neural Control for Epidemic Model of Covid-19 with a Complex Network Approach. IEEE Latin America Transactions, 19(6), 866–873. Retrieved from https://latamt.ieeer9.org/index.php/transactions/article/view/4175

Issue

Vol. 19 No. 6 (2021): Special Issue on Fighting Against COVID-19

Section

Special Issue on Fighting against COVID-19