The probabilistic behavior of the set and reset thresholds in Knowm's SDC memristors: Characterization and Simulation

Authors

  • Gerardo Abel Laguna-Sanchez Universidad Autonoma Metropolitana, Mexico City https://orcid.org/0000-0001-5145-1248
  • Miguel Lopez-Guerrero Universidad Autonoma Metropolitana, Unidad Iztapalapa, Mexico City https://orcid.org/0000-0001-5987-8780
  • Ricardo Barron-Fernandez Centro de Investigación en Computacion del Instituto Politecnico Nacional, Mexico City

Keywords:

Alpha-stable random variable characterization, SDC memristor modeling, SDC memristor simulating

Abstract

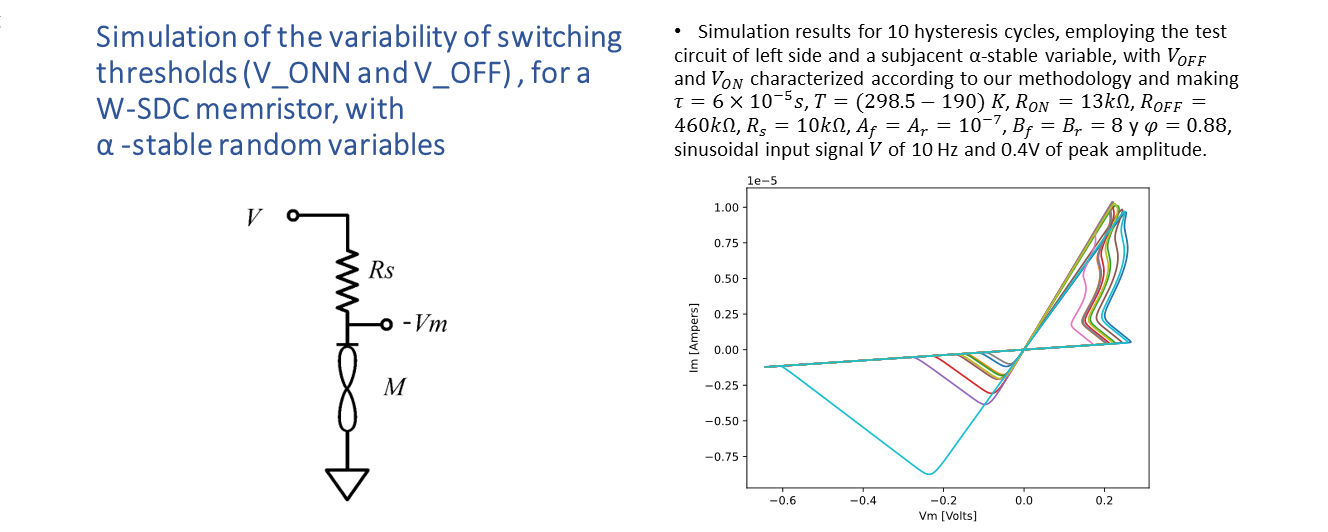
This paper presents a proposal for the characterization of the set and reset thresholds for Knowm’s SDC memristors. The purpose is to incorporate the variability of the hysteresis cycles within the Generalized Mean Metastable Switch (GMMS) memristor model and, in this way, be able to perform simulations that reproduce these phenomena in a meaningful and computationally efficient way. We depart from the assumption that their probabilistic behavior can be well represented by using α-stable random variables. The main advantage of using α-stable variables is that they can capture both skewness and high variability (i.e., heavy tails), which can be exhibited by the observed phenomenon. At the same time, they also include the Gaussian random variable as a particular case, thus increasing the modeling flexibility.

Downloads

Download data is not yet available.

Author Biographies

Gerardo Abel Laguna-Sanchez, Universidad Autonoma Metropolitana, Mexico City

Gerardo Laguna-Sanchez (Senior Member, IEEE) received the Ph.D. degree from National Polytechnic Institute (CIC-IPN, Mexico City) in 2010, the M.Sc. degree from National Autonomous University of Mexico (DEPFI-UNAM, Mexico City) in 1998; and the Electronic/Computer Engineering B.Sc. degree from Metropolitan Autonomous University (UAM, Mexico City) in 1993, Mexico City. Currently he is with Department of Information and Communication Systems at Metropolitan Autonomous University (UAM-Lerma), Lerma de Villada County. His research interests include digital communications, AI and advanced signal processing applications.

Miguel Lopez-Guerrero, Universidad Autonoma Metropolitana, Unidad Iztapalapa, Mexico City

Miguel Lopez-Guerrero received his Ph.D. in Electrical Engineering from the University of Ottawa in 2004. He received his M.Sc. in Electrical Engineering in 1998 and the B.Sc. in Mechanical-Electrical Engineering in 1995, both from the National Autonomous University of Mexico. He is an Associate Professor with the Metropolitan Autonomous University (Mexico City). His research interests span several aspects of telecommunication networks including network traffic modeling, medium access control and mobility-related studies.

Ricardo Barron-Fernandez, Centro de Investigación en Computacion del Instituto Politecnico Nacional, Mexico City

Ricardo Barron-Fernandez received the Ph.D. degree and the M.Sc. degree from Center for Computer Research (CIC) at National Polytechnic Institute (IPN, Mexico City), and the Mathematics B.Sc. from Autonomous University of Mexico (UNAM, Mexico City). Currently he is with AI Laboratory at CIC. His research interests are applications of mathematics in computer science.

References

L. Chua, “Memristor-The missing circuit element,” IEEE Transactions on Circuit Theory, vol. 18, no. 5, pp. 597–519, 1971. https://doi.org/10.1109/TCT.1971.1083337.

D. Strukov et al., “The missing memristor found,” Nature, vol. 453, pp. 80–83, 2008. https://doi.org/10.1038/nature06932.

C. Choi, “Brainwave: If memristors act like neurons, put them in neural networks.” Online IEEE Spectrum, 2021. https://spectrum.ieee.org/memristor-random.

A. Nugent and T. Molter, “AHaH computing–from metastable switches to attractors to machine learning,” PLOS ONE, vol. 9, no. 2, 2014. https://doi.org/10.1371/journal.pone.0085175.

H. Jaeger, “Towards a generalized theory comprising digital, neuromorphic and unconventional computing,” Neuromorphic Computing and Engineering, vol. 1, no. 1, p. 012002, 2021. https://doi.org/10.1088/2634-4386/abf151.

S. Kumar et al., “Third-order nanocircuit elements for neuromorphic engineering,” Nature, vol. 585, pp. 518–523, 2020. https://doi.org/10.1038/s41586-020-2735-5.

Y. Hosoi et al., “High speed unipolar switching resistance RAM (RRAM) technology,” in 2006 International Electron Devices Meeting, pp. 1–4, 2006. https://doi.org/10.1109/IEDM.2006.346732.

S. Raoux, W. Welnic, and D. Ielmini, “Phase change materials and their application to nonvolatile memories,” Chemical Reviews, vol. 110, no. 1, pp. 240–267, 2010. https://doi.org/10.1021/cr900040x.

K. Campbell, “Self-directed channel memristor for high temperature operation,” Microelectronics journal, vol. 59, pp. 10–14, 2017. https://doi.org/10.1016/j.mejo.2016.11.006.

K. Drake et al., “Comparison of the electrical response of Cu and Ag ion-conducting SDC memristors over the temperature range 6 k to 300 k,” Micromachines, vol. 10, no. 10:663, 2019. https://doi.org/10.3390/mi10100663.

X. Guan, S. Yu, and H.-S. Wong, “On the switching parameter variation of metal-oxide RRAM—Part I: Physical modeling and simulation methodology,” IEEE Transactions on Electron Devices, vol. 59, no. 4, pp. 1172–1182, 2012. https://doi.org/10.1109/TED.2012.2184545.

S. Ambrogio et al., “Statistical fluctuations in HfOx resistive-switching memory: Part I - set/reset variability,” IEEE Transactions on Electron Devices, vol. 61, no. 8, pp. 2912–2919, 2014. https://doi.org/10.1109/TED.2014.2330200.

L. Gao et al., “Memristor modeling: challenges in theories, simulations, and device variability,” Journal of Materials Chemistry C, vol. 9, pp. 16859–16884, 2021. https://doi.org/10.1039/D1TC04201G.

A. Nugent, Knowm Memristor Discovery Manual. Knowm, Santa Fe, NM., 2020.

R. Carboni and D. Ielmini, “Stochastic memory devices for security and computing,” Advanced Electronic Materials, vol. 5, no. 9, 2019. https://doi.org/10.1002/aelm.201900198.

A. Mizrahi et al., Memristive Devices for Brain-Inspired Computing, ch. Exploiting the stochasticity of memristive devices for computing. Woodhead Publishing, 2020. https://doi.org/10.1016/B978-0-08-102782-0.00011-3.

M. Hu et al., “The stochastic modeling of TiO2 memristor and its usage in neuromorphic system design,” in 19th Asia and South Pacific Design Automation Conference (ASP-DAC), pp. 831–836, 2014. https://doi.org/10.1109/ASPDAC.2014.6742993.

R. Naous et al., “Stochasticity modeling in memristors,” IEEE Transactions on Nanotechnology, vol. 15, no. 1, pp. 15–28, 2016. https://doi.org/10.1109/TNANO.2015.2493960.

S. Stathopoulos, “A memristive switching uncertainty model,” IEEE Transactions on Electronic Devices, vol. 66, no. 7, pp. 2946–2953, 2019. https://doi.org/10.1109/TED.2019.2918102.

F. Alonso et al., “Memristor variability and stochastic physical properties modeling from a multivariate time series approach,” Chaos, Solitons and Fractals, vol. 143, p. 110461, 2021. https://doi.org/10.1016/j.chaos.2020.110461.

N. Agudov et al., “Nonstationary distributions and relaxation times in a stochastic model of memristor,” Journal of Statistical Mechanics, p. 024003, 2020. https://doi.org/10.1088/1742-5468/ab684a.

N. Agudov et al., “Stochastic model of memristor based on the length of conductive region,” Chaos, Solitons and Fractals, vol. 150, p. 111131, 2021. https://doi.org/10.1016/j.chaos.2021.111131.

V. Ostrovskii et al., “Structural and parametric identification of Knowm memristors,” Nanomaterials, vol. 12, no. 1:63, pp. 1–20, 2022. https://doi.org/10.3390/nano12010063.

T. Driscoll et al., “Chaotic memristor,” Applied Physics A, vol. 102, pp. 885–889, 2011. https://doi.org/10.1007/s00339-011-6318-z.

C. Fernandez et al., “Comprehensive predictive modeling of resistive switching devices using a bias-dependent window function approach,” Solid-State Electronics, vol. 170, p. 107833, 2020. https://doi.org/10.1016/j.sse.2020.107833.

J. Riquelme et al., “RevI-Ve: A comprehensive software interface for easy ReRAM device characterization,” in 2023 12th International Conference on Modern Circuits and Systems Technologies, pp. 1–4, 2023. https://doi.org/10.1109/MOCAST57943.2023.10176900.

T. Molter and A. Nugent, “The mean metastable switch memristor model in Xyce,” 2017. https://knowm.org/the-mean-metastable-switch-memristor-model-in-xyce/.

B. Garda, “Modeling of memristors under periodic signals of different parameters,” Energies, vol. 14, no. 21:7264, pp. 1–15, 2021. https://doi.org/10.3390/en14217264.

G. Laguna-Sanchez, “Alpha-stable based stochastic GMMS memristor model.” GitHub Repository, 2022. https://github.com/galaguna/Stochastic_GMMS_memristor_model.

Knowm, Santa Fe, NM., Knowm Self Directed Channel Memristors, Data Sheet Rev. 3.2, 2019. https://knowm.org/downloads/Knowm_Memristors.pdf.

S. Kogon and D. Williams, “On the characterization of impulsive noise with α-stable distributions using fourier techniques,” in Proceedings of the 29th Asilomar Conference on Signals, Systems and Computers, pp. 787–791, 1995.

G. Samorodnitsky and M. Taqqu, Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance. Chapman & Hall/CRC, 1994.

I. Koutrouvelis, “An iterative procedure for the estimation of the parameters of stable laws,” Communication Statistical Simulation Computation, vol. 10, pp. 17–28, 1981. https://doi.org/10.1080/03610918108812189.

G. Laguna-Sanchez and M. Lopez-Guerrero, “On the use of Alpha-Stable distributions in noise modeling for PLC,” IEEE Transactions on Power Delivery, vol. 30, no. 4, pp. 1863–1870, 2015. https://doi.org/10.1109/TPWRD.2015.2390134.

D. Scott, “On optimal and data-based histograms,” Biometrika, vol. 66, no. 3, pp. 605–610, 1979. https://doi.org/10.2307/2335182.

Downloads

Published

2023-11-01

How to Cite

Laguna-Sanchez, G. A., Lopez-Guerrero, M., & Barron-Fernandez, R. (2023). The probabilistic behavior of the set and reset thresholds in Knowm’s SDC memristors: Characterization and Simulation. IEEE Latin America Transactions, 21(12), 1266–1274. Retrieved from https://latamt.ieeer9.org/index.php/transactions/article/view/8308

Issue

Vol. 21 No. 12 (2023): Ordinary Issue

Section

Computing