Learning Decision Variables in Many-Objective Optimization Problems
Keywords:
Many-Objective Optimization, Machine Learning, Inverse Surrogate Models, Decision Variable LearningAbstract
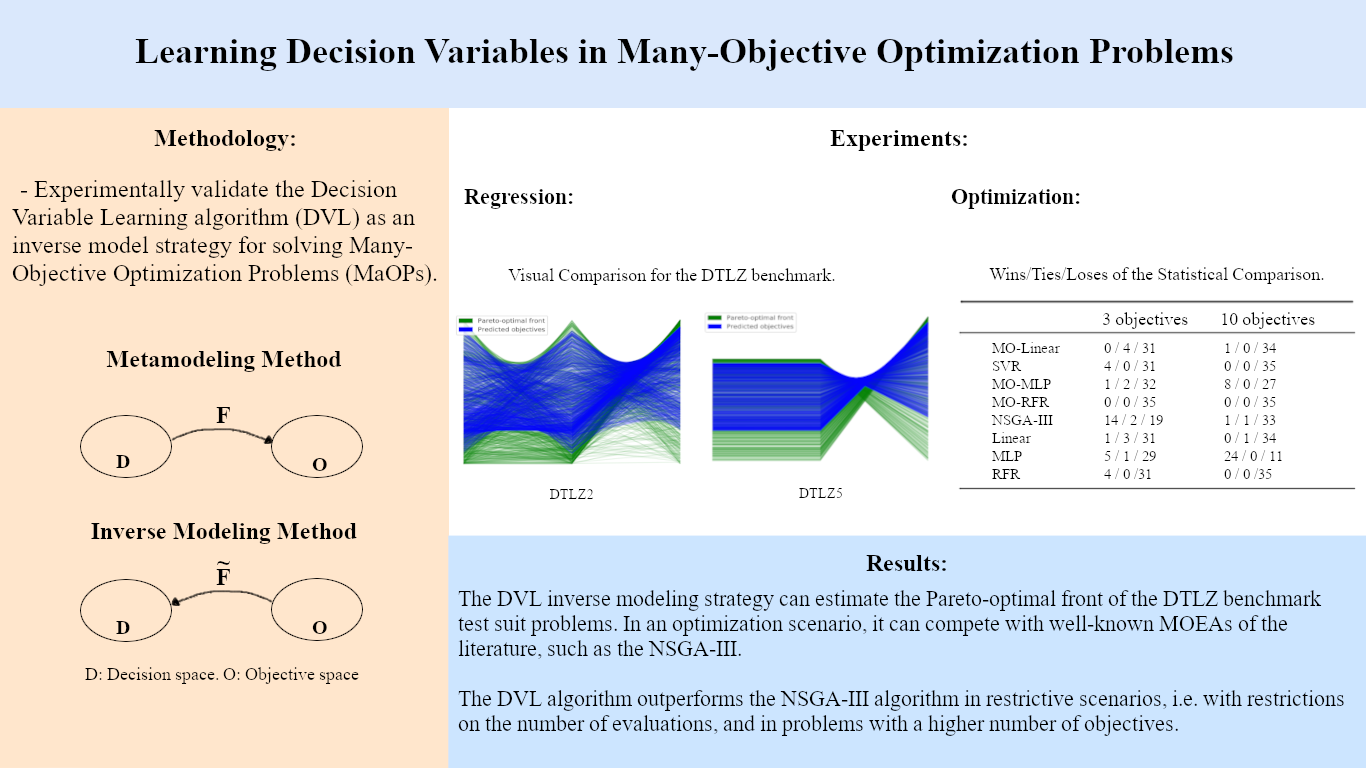
Traditional Multi-Objective Evolutionary Algorithms (MOEAs) have shown poor scalability in solving Many-Objective Optimization Problems (MaOPs). The use of machine learning techniques to enhance optimization algorithms applied to MaOPs has been drawing attention due to their ability to add domain knowledge during the search process. One method of this kind is inverse modeling, which uses machine learning models to enhance MOEAs differently, mapping the objective function values to the decision variables. The Decision Variable Learning (DVL) algorithm uses the inverse model in its concept and has shown good performance due to the ability to directly predict solutions closed to the Pareto-optimal front. The main goal of this work is to experimentally show the DVL as an optimization algorithm for MaOPs. Our results demonstrate that the DVL algorithm outperformed the NSGA-III, a well-known MOEA from the literature, in almost all scenarios with restriction on the number of objective functions with a high number of objectives.
Downloads
References
O. Schütze, A. Lara, and C. A. C. Coello, “On the influence of the
number of objectives on the hardness of a multiobjective optimization
problem,” IEEE Trans. Evolutionary Computation, vol. 15, no. 4,
pp. 444–455, 2011.
L. Calvet, J. de Armas, D. Masip, and A. A. Juan, “Learnheuristics:
hybridizing metaheuristics with machine learning for optimization with
dynamic inputs,” Open Mathematics, vol. 15, no. 1, pp. 261–280, 2017.
L. Shi and K. Rasheed, “A survey of fitness approximation methods
applied in evolutionary algorithms,” in Computational intelligence in
expensive optimization problems, pp. 3–28, Springer, 2010.
I. Giagkiozis and P. J. Fleming, “Pareto front estimation for decision
making,” Evolutionary computation, vol. 22, no. 4, pp. 651–678, 2014.
M. Santos, J. A. de Oliveira, and A. Britto, “Decision variable learning,”
in 2019 8th Brazilian Conference on Intelligent Systems (BRACIS),
pp. 497–502, IEEE, 2019.
R. L. Iman, J. M. Davenport, and D. K. Zeigler, Latin hypercube
sampling (program user’s guide). Department of Energy, Sandia
Laboratories, 1980.
K. Deb and H. Jain, “An evolutionary many-objective optimization
algorithm using reference-point-based nondominated sorting approach,
part i: Solving problems with box constraints,” IEEE Transactions on
Evolutionary Computation, vol. 18, no. 4, pp. 577–601, 2014.
R. Kudikala, I. Giagkiozis, and P. Fleming, “Increasing the density
of multi-objective multi-modal solutions using clustering and pareto
estimation techniques,” in The 2013 World Congress in Computer
Science Computer Engineering and Applied Computing, 2013.
Y. Yan, I. Giagkiozis, and P. J. Fleming, “Improved sampling of
decision space for pareto estimation,” in Proceedings of the 2015 Annual
Conference on Genetic and Evolutionary Computation, pp. 767–774,
R. Cheng, Y. Jin, K. Narukawa, and B. Sendhoff, “A multiobjective
evolutionary algorithm using gaussian process-based inverse model-
ing,” IEEE Transactions on Evolutionary Computation, vol. 19, no. 6,
pp. 838–856, 2015.
I. Das and J. E. Dennis, “Normal-boundary intersection: A new method
for generating the pareto surface in nonlinear multicriteria optimization
problems,” SIAM journal on optimization, vol. 8, no. 3, pp. 631–657,
K. Deb, L. Thiele, M. Laumanns, and E. Zitzler, “Scalable test problems
for evolutionary multiobjective optimization,” in Evolutionary multiob-
jective optimization, pp. 105–145, Springer, 2005.