A Fuzzy Approach to Drum Cymbals Classification

Authors

Keywords:

Cymbals, Bronze Alloys, Music Information Retrieval, Fuzzy

Abstract

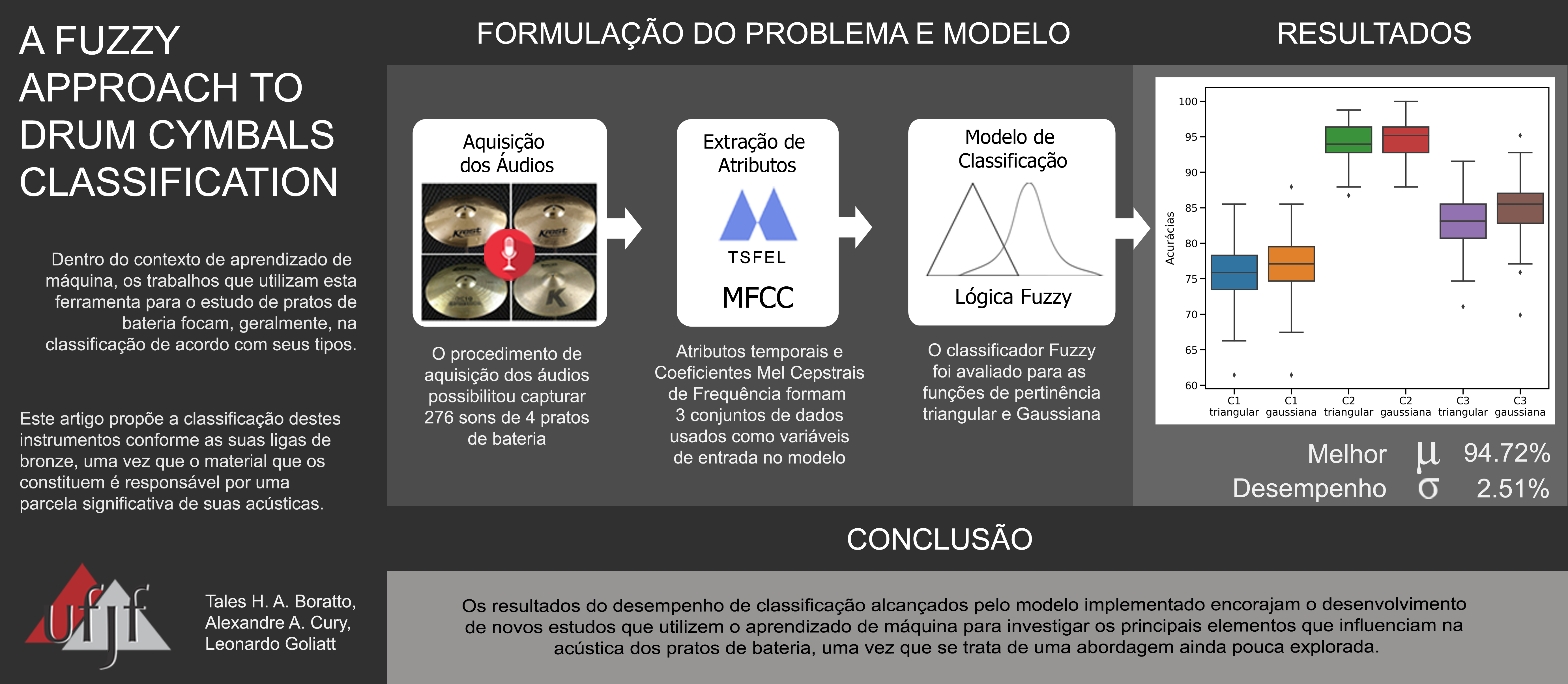
The many factors that influence the sound of a cymbal, combined with the external aspects that modify its sound perception, make the study of the acoustics of these instruments more challenging. Within the context of machine learning, most researches involving cymbal classification from their sounds aim to identify those instruments according to their types. However, there is a lack of studies investigating the acoustic elements of cymbals using machine learning techniques as tools. Hence, this paper proposes to classify cymbals according to their constitutive materials, since the metallic alloy assumes a significant portion is responsible for their acoustics. In addition, there is an interest in evaluating a fuzzy logic approach as a classifier applied to three sets of attributes, formed from temporal features and Mel Frequency Cepstral Coefficients extracted from audio signals, comparing triangular and Gaussian membership functions. For this, 276 audios, referring to 4 drum cymbals, were collected from a standardized procedure for capturing the sounds that considered variations in microphones and environments. As a result, the implemented model achieved 94.72% of average accuracy with a standard deviation of 2.51%, considering the Gaussian membership function and Mel Frequency Cepstral Coefficients as the audio descriptor.

Downloads

Download data is not yet available.

Author Biographies

Tales Boratto, Federal University of Juiz de Fora

Mestrando em Modelagem Computacional pela Universidade Federal de Juiz de Fora. Possui graduação em Ciências Exatas (2019) e em Engenharia Mecânica (2020) pela Universidade Federal de Juiz de Fora. Suas pesquisas envolvem as áreas de Ciência dos Materiais, com ênfase em Ligas de Bronze, Processos de Fabricação, Recuperação de Informação Musical (MIR) e Aprendizado de Máquina.

Alexandre Cury, Federal University of Juiz de Fora

Graduado em Engenharia Civil pela Universidade Federal de Juiz de Fora (2006), mestre em Modelagem Computacional pela Universidade Federal de Juiz de Fora (2008) e doutor em Engenharia Civil pela Universidade Paris-Est (École Nationale des Ponts et Chaussées) em 2010. Atua, principalmente, nos seguintes temas: monitoramento de integridade estrutural, análise de vibrações, detecção de danos, identificação modal, análise estatística avançada e confiabilidade estrutural. É professor associado no Departamento de Mecânica Aplicada e Computacional. Foi coordenador da APCN e do Programa de Pós-Graduação em Engenharia Civil da Universidade Federal de Juiz de Fora (2016-2019). Entre 2014 e 2016, foi membro da CA-TEC (Câmara de Assessoramento de Arquitetura e Engenharias) da FAPEMIG (Fundação de Amparo a Pesquisa do Estado de Minas Gerais). É Pesquisador de Produtividade do CNPq desde 2013. Membro do corpo editorial da revista Frontiers: Build Engineering e Structural Sensing. Recebeu menção honrosa no Prêmio CAPES de Tese 2017.

Leonardo Goliatt, Federal University of Juiz de Fora

Possui graduação em Engenharia Civil pela Universidade Federal de Juiz de Fora (2003) e Doutorado em Modelagem Computacional pelo Laboratório Nacional de Computação Científica (2009). Atuou como professor do Departamento de Ciências Matemáticas e Naturais da Universidade Federal do Espírito Santo (2010). Professor associado do Departamento de Mecânica Aplicada e Computacional e membro permanente do Programa de Pós-Graduação em Modelagem Computacional da Universidade Federal de Juiz de Fora. Atuou como chefe do Departamento de Mecânica Aplicada e Computacional (2014-2016). Membro da Comissão Própria de Avaliação da UFJF (2017-2019) e coordenador do Programa de Pós-Graduação em Modelagem Computacional da UFJF (2018-2021).
Tem experiência na área de Computação Evolucionária, Inteligência Computacional e Ciência de Dados, atuando principalmente nos seguintes temas: aprendizado de máquina, meta heurísticas, metamodelos, otimização estrutural e simulação.

References

T. H. A. Boratto, R. F. Marcomini, L. Goliatt, C. R. Pagotto, A. A. Cury, I. J. U. Pereira, and F. D. Nishida, “Análise dos efeitos de dois diferentes métodos de fabricação em pratos de bateria,” in XI Congresso

Brasileiro de Engenharia de Fabricação (COBEF), 2021.

T. Rossing, Springer handbook of acoustics. Springer Handbooks, New York, NY: Springer New York, 2nd ed., 2014.

J. J. Harrison and A. J. Hill, “A scientific approach to microphone placement for cymbals in live sound,” 2013.

H. Pinksterboer and R. Mattingly, The Cymbal Book. Musical Instruments Series, Hal Leonard Publishing Corporation, 1992.

K. Osamura, F. Kuratani, T. Koide, W. Ogawa, H. Taniguchi, Y. Monju, T. Mizuta, and T. Shobu, “The correlation between the percussive sound and the residual stress/strain distributions in a cymbal,” Journal of Materials Engineering and Performance, vol. 25, 10 2016.

F. Kuratani, T. Yoshida, T. Koide, T. Mizuta, and K. Osamura, “Understanding the effect of hammering process on the vibration characteristics of cymbals,” Journal of Physics: Conference Series, vol. 744, p. 012110, sep 2016.

W. OGAWA, F. KURATANI, T. YOSHIDA, T. KOIDE, and T. MIZUTA, “Effect of bell size on sound characteristics of cymbals,” Transactions of the JSME (in Japanese), vol. 86, no. 881, pp. 19–00237–19–00237, 2020.

S. Slamet, D. Suyitno, I. Kusumaningtyas, and I. Miasa, “Effect of high-tin bronze composition on physical, mechanical, and acoustic properties of gamelan materials,” 08 2021.591

I. K. G. Sugita, R. Soekrisno, and D. Suyitno, “Mechanical and damping properties of silicon bronze alloys for music applications,” Int J Eng & Technol IJET-IJENS, vol. 11, pp. 98–105, 01 2011.

T. M. Mitchell, Machine Learning. MGH, 1997.

P. Herrera, A. Yeterian, and F. Gouyon, “Automatic classification of drum sounds: A comparison of feature selection methods and classification techniques,” in Music and Artificial Intelligence (C. Anagnostopoulou, M. Ferrand, and A. Smaill, eds.), (Berlin, Heidelberg), pp. 69–80, Springer Berlin Heidelberg, 2002.

J. G. Cleary and L. E. Trigg, “K*: An instance-based learner using an entropic distance measure,” in Machine Learning Proceedings 1995 (A. Prieditis and S. Russell, eds.), pp. 108–114, San Francisco (CA):

Morgan Kaufmann, 1995.

S. Cavaco and H. Almeida, “Automatic cymbal classification using non-negative matrix factorization,” in 2012 19th International Conference on Systems, Signals and Image Processing (IWSSIP), pp. 468–471, 2012.

V. M. A. Souza, G. E. A. P. A. Batista, and N. E. Souza-Filho, “Automatic classification of drum sounds with indefinite pitch,” in Proceedings of International Joint Conference on Neural Networks

(IJCNN), 2015.

B. Y. George J. Klir, Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, 1995.

B. Logan, “Mel frequency cepstral coefficients for music modeling,” Proc. 1st Int. Symposium Music Information Retrieval, 11 2000.

M. Slaney, “Auditory Toolbox Version 2,” Technical Report #1998-010, Interval Research Corporation, 1998.

AKG, “C414 XLII - Reference multipattern condenser microphone.” Last accessed 28 March 2021.

Shure, “PGA81 - Microfone condensador cardioide para instrumento.” Last accessed 02 April 2021.

M. Barandas, D. Folgado, L. Fernandes, S. Santos, M. Abreu, P. Bota, H. Liu, T. Schultz, and H. Gamboa, “Tsfel: Time series feature extraction library,” SoftwareX, vol. 11, p. 100456, 2020.

A. V. Oppenheim and R. W. Schafer, “From frequency to quefrency: a history of the cepstrum,” IEEE Signal Processing Magazine, vol. 21, no. 5, pp. 95–106, 2004.

L. Muda, M. Begam, and I. Elamvazuthi, “Voice recognition algorithms using mel frequency cepstral coefficient (MFCC) and dynamic time warping (DTW) techniques,” CoRR, vol. abs/1003.4083, 2010.

D. Bhalke, C. R. Rao, and D. Bormane, “Hybridisation of mel frequency cepstral coefficient and higher order spectral features for musical instruments classification,” Archives of Acoustics, vol. 41, no. 3, 2016.

R. Loughran, J. Walker, M. O’Farrell, and M. O’Neill, “Comparison of features in musical instrument identification using artificial neural networks,” in 5th International Symposium on Computer Music Modeling and Retrieval., pp. 19–33, Springer, 2008.

R. Loughran, J. Walker, M. O’Neill, and M. O’Farrell, “The use of mel-frequency cepstral coefficients in musical instrument identification,” Feb 2018.

M. Malík and R. Orješek, “The comparison of selected audio features and classification techniques in the task of the musical instrument,” 05 2016.

M. S. Nagawade and V. R. Ratnaparkhe, “Musical instrument identification using mfcc,” in 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information Communication Technology (RTEICT), pp. 2198–2202, 2017.

MATLAB, “Extract cepstral features from audio segment.” Last accessed 28 April 2021.

Alan V. Oppenheim, Ronald W. Schafer, and John R. Buck, Discrete-Time Signal Processing. Prentice-Hall Signal Processing Series, Prentice Hall, 2nd ed ed., 1999.

J. P. Crutchfield and D. P. Feldman, “Regularities unseen, randomness observed: Levels of entropy convergence,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 13, no. 1, pp. 25–54, 2003.

L. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965.

V. Cherkassky, “Fuzzy inference systems: A critical review,” in Computational Intelligence: Soft Computing and Fuzzy-Neuro Integration with Applications (O. Kaynak, L. A. Zadeh, B. Türk ̧sen, and I. J. Rudas, eds.), (Berlin, Heidelberg), pp. 177–197, Springer Berlin Heidelberg, 1998.662

E. M. Jyh-Shing Roger Jang, Chuen-Tsai Sun, Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence. Prentice Hall, 1 ed., 1997.

Wes McKinney, “Data Structures for Statistical Computing in Python,” in Proceedings of the 9th Python in Science Conference (Stéfan van der Walt and Jarrod Millman, eds.), pp. 56 – 61, 2010.

C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del R’ıo, M. Wiebe, P. Peterson, P. G’erard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke, and T. E. Oliphant, “Array programming with NumPy,” Nature, vol. 585, pp. 357–362, Sept. 2020.

F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, et al., “Scikit-learn: Machine learning in python,” The Journal of Machine Learning Research, vol. 12, pp. 2825–2830, 2011.

M. L. Waskom, “seaborn: statistical data visualization,” Journal of Open Source Software, vol. 6, no. 60, p. 3021, 2021.

P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J.

Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, ̇I. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro,

F. Pedregosa, P. van Mulbregt, and SciPy 1.0 Contributors, “SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python,” Nature Methods, vol. 17, pp. 261–272, 2020.

T. H. Boratto, A. Cury, and L. Goliatt, “Crash cymbal sounds.” https://data.mendeley.com/datasets/9tytvdxd24/1, 2022.

A. Géron, Hands-On Machine Learning with Scikit-Learn and Tensor-Flow: Concepts, Tools, and Techniques to Build Intelligent Systems. O’Reilly Media, 1 ed., 2017.

Downloads

Published

2022-06-27

How to Cite

Boratto, T., Cury, A., & Goliatt, L. (2022). A Fuzzy Approach to Drum Cymbals Classification. IEEE Latin America Transactions, 20(9), 2172–2180. Retrieved from https://latamt.ieeer9.org/index.php/transactions/article/view/6487

Issue

Vol. 20 No. 9 (2022): Ordinary Issue

Section

Computing