A Comparative Study of Time Domain Compressed Sensing Techniques for Optoacoustic Imaging
Keywords:
optoacoustic imaging, compressed sensing, time domain models, reconstruction algorithmsAbstract
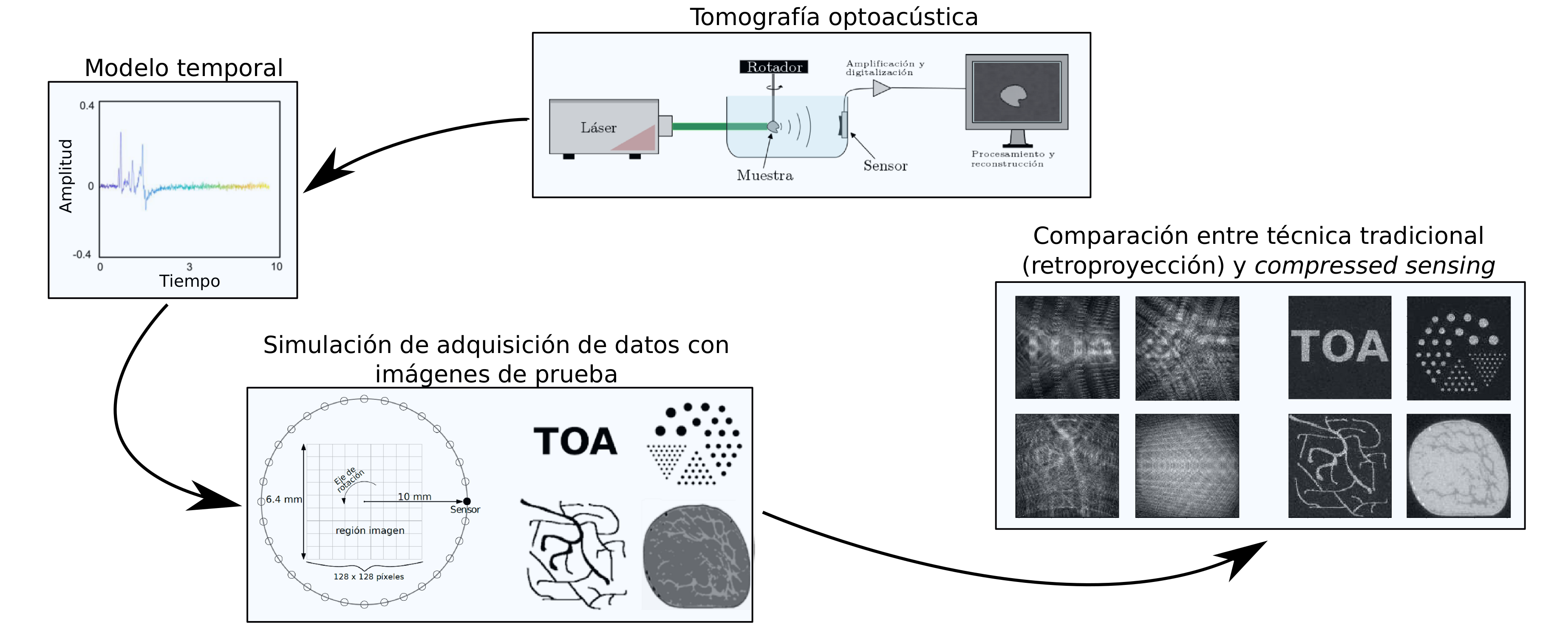
Speeding up data acquisition and reducing the complexity of the detection system are among the central goals for advancing optoacoustic imaging. In this way, new reconstruction algorithms using the compressed sensing (CS) formalism have received considerable interest in recent years. This work presents a comparative study of reconstruction algorithms using time-domain CS schemes for optoacoustic tomography. This is motivated by the well-known capabilities of the CS paradigm in achieving good reconstruction performance even with limited sensing capabilities. Formulation of the mathematical problem is provided along with simulation results, where the performance of different representation basis used in time-domain CS strategies are analyzed in a qualitative and quantitative fashion. Comparison with a well-established optoacoustic tomography reconstruction technique as backprojection is also provided. These experiments show the suitability of time-domain CS techniques for this application and point out that the use of the canonical basis for the representation of the optoacoustic measurements is well suited in comparison with other more sophisticated basis.
Downloads
References
M. Xu and L. Wang, “Photoacoustic imaging in biomedicine,” Rev. Sci. Instrum., vol. 77, p. 041101, 2006.
X. Wang, R. Witte, and H. Xin, “Thermoacoustic and photoacoustic characterizations of few-layer graphene by pulsed excitations,” Appl Phys Lett., vol. 108, p. 143104, 2016.
H. Moon, D. Kumar, H. Kim, C. Sim, J. Chang, J. Kin, , H. Kim, and D. Lim, “Amplified photoacoustic performance and enhanced photothermal stability of reduced graphene oxide coated gold nanorods for sensitive photoacoustic imaging,” Appl Phys Lett., vol. 9, pp. 2711–2719, 2015.
M. G. Gonzalez, E. Acosta, and G. Santiago, “Simple method to determine the resolution and sensitivity of systems for optoacoustic tomography,” Elektron, vol. 2, pp. 63–66, 2018.
G. Paltauf, P. Hartmair, G. Kovachev, and R. Nuster, “Piezoelectric line detector array for photoacoustic tomography,” Photoacoustics, vol. 8, pp. 28–36, 2017.
A. Rosenthal, V. Ntziachristos, and D. Razansky, “Acoustic inversion in optoacoustic tomography: A review,” Current Medical Imaging Reviews, vol. 9, pp. 318–336, 2013.
M. Xu and L. Wang, “Universal back-projection algorithm for photoacoustic computed tomography,” Phys. Rev. E, vol. 71, p. 016706, 2005.
P. Burgholzer, J. Bauer-Marschallinger, H. Gruen, M. Haltmeier, and G. Paltauf, “Temporal back-projection algorithms for photoacoustic tomography with integrating line detectors,” Inverse Probl., vol. 23, no. 6, pp. S65–S80, 2007.
P. M. Rocca, L. C. Brazzano, E. Acosta, and M. G. Gonzalez, “Optoacoustic imaging algorithms: Effect of piezoelectric wideband sensors,” Elektron, vol. 1, no. 2, pp. 58–65, 2017.
A. Fatima, R. Manwar, M. Zafar, R. Zang, B. Huang, N. Dadashzadeh, J. Xia, and K. Avanaki, “Review of cost reduction methods in photoacoustic computed tomography,” Photoacoustics, vol. 15, p. 100137, 2019.
J. Bauer-Marschallinger, K. Felbermayer, and T. Berer, “All-optical photoacoustic projection imaging,” J. Biomed. Opt. Express, vol. 8, no. 9, pp. 3938–3951, 2017.
J. Meng, C. Liu, J. Kim, C. Kim, and L. Song, “Compressed sensing with a gaussian scale mixture model for limited view photoacoustic computed tomography in vivo,” Tech. in Cancer Research and Treatment, vol. 17, pp. 1–11, 2018.
E. J. Cand`es, J. Romberg, and T. Tao, “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Trans. Inf. Theory, vol. 52, no. 2, p. 489–509, 2006.
Y. Yang, F. Liu, W. Xu, and S. Crozier, “Compressed sensing mri via two-stage reconstruction,” IEEE Trans Biomed Eng., vol. 62, pp. 110–118, 2015.
J. Provost and F. Lesage, “The application of compressed sensing for photo-acoustic tomography,” IEEE Trans Med Imaging., vol. 28, pp. 585–594, 2009.
D. Liang, H. Zhang, and L. Ying, “Compressed-sensing photoacoustic imaging based on random optical illumination,” Int. J. Functional Informatics and Personalised Medicine, vol. 2, pp. 394–406, 2009.
Z. Guo, C. Li, L. Song, and et al., “Compressed sensing in photoacoustic tomography in vivo,” J Biomed Opt., vol. 15, p. 021311, 2010.
J. Meng, L. Wang, D. Liang, and et al., “Compressed-sensing photoacoutic computed tomography in vivo with partially known support,” Opt Express, vol. 20, pp. 16 510–16 522, 2012.
Y. Guo, B. Li, and X. Yin, “Single-shot compressed photoacoustic tomographic imaging with a single detector in a scattering medium,” Phys. Rev. Applied, vol. 13, p. 044009, Apr 2020.
J. Meng, D. Liang, and L. Song, “Compressed sensing photoacoustic tomography in vivo in time and frequency domains,” in Proceedings of 2012 IEEE-EMBS International Conference on Biomedical and Health Informatics, 2012, pp. 717-720.
A. Hauptmann and B. Cox, “Deep learning in photoacoustic tomography: current approaches and future directions,” Journal of Biomedical Optics, vol. 25, no. 11, pp. 1 – 46, 2020.
C. Tian, M. Pei, K. Shen, S. Liu, Z. Hu, and T. Feng, “Impact of system factors on the performance of photoacoustic tomography scanners,” Phys. Rev. Applied, vol. 13, p. 014001, 2020.
J. Tick, A. Pulkkinen, and T. Tarvainen, “Modelling of errors due to speed of sound variations in photoacoustic tomography using a bayesian framework,” Biomed. Phys. Eng. Express, vol. 6, p. 015003, 2019.
K. Mitsuhashi, K. Wang, and M. Anastasio, “Investigation of the far field approximation for modeling a transducer’s spatial impulse response in photoacoustic computed tomography,” Photoacoustics, vol. 2, pp. 21–32, 2014.
L. Hirsch, M. G. Gonzalez, and L. R. Vega, “On the robustness of model-based algorithms for photoacoustic tomography: comparison between time and frequency domains,” Rev. Sci. Instrum., vol. 92, p. 114901, 11 2021.
C. Lutzweiler and D. Razansky, “Optoacoustic imaging and tomography: reconstruction approaches and outstanding challenges in image performance and quantification,” Sensors, vol. 13, pp. 7345–7384, 2013.
L. V. Wang and H. Wu, Biomedical Optics: Principles and Imaging. John Wiley & Sons, 2009.
M. Cui, H. Zuo, X. Wang, K. Deng, J. Luo, and C. Ma, “Adaptive photoacoustic computed tomography,” Photoacoustics, vol. 21, p. 100223, 2021.
A. Rosenthal, D. Razansky, and V. Ntziachristos, “Fast semi-analytical model-based acoustic inversion for quantitative optoacoustic tomography,” IEEE Trans Med Imaging, vol. 29, no. 6, pp. 1275–1285, 2010.
G. Paltauf, P. R. Torke, and R. Nuster, “Modeling photoacoustic imaging with a scanning focused detector using monte carlo simulation of energy deposition,” Journal of biomedical optics, vol. 23, no. 12, 2018.
G. Paltauf, J. Viator, S. Prahla, and S. Jacques, “Iterative reconstruction algorithm for optoacoustic imaging,” The Journal of the Acoustical Society of America, vol. 112, no. 4, pp. 1536–1544, 2002.
X. Dean-Ben, A. Buehler, V. Ntziachristos, and D. Razansky, “Accurate model-based reconstruction algorithm for three-dimensional optoacoustic tomography,” IEEE Trans Med Imaging, vol. 31, no. 10, pp. 1922-1928, 2012.
S. Foucart and H. Rauhut, A Mathematical Introduction to Compressive Sensing. Springer, 2013.
E. J. Candes and M. B. Wakin, “An introduction to compressive sampling,” IEEE Signal Processing Magazine, vol. 25, no. 2, pp. 21–30, March 2008.
M. Banait, S. Dhok, and R. Deshmukh, “A systematic review of compressive sensing: Concepts, implementations and applications,” IEEE Access, vol. PP, pp. 1–1, 01 2018.
M. Osborne, B. Presnell, and B. Turlach, “On the lasso and its dual,” J. Computat. Graphical Stat., vol. 9, pp. 319–337, 2000.
A. Sharma, S. Kalva, and M. Pramanik, “A comparative study of continuous versus stop-and-go scanning in circular scanning photoacoustic tomography,” IEEE J. Sel. Top. Quantum Electron, vol. 25, no. 1, pp. 1–9, 2019.
M. Haltmeier, M. Sandbichler, T. Berer, J. Bauer-Marschallinger, P. Burgholzer, and L. Nguyen, “A sparsification and reconstruction strategy for compressed sensing photoacoustic tomography,” Acoust. Soc. Am., vol. 143, no. 6, p. 3838–3848, 2018.
J.-L. Starck, Sparse Image and Signal Processing: Wavelets and Related Geometric Multiscale Analysis, Second Edition, 2nd ed. Cambridge University Press, Oct 2015.
N. Awasthi, G. Jain, S. K. Kalva, M. Pramanik, and P. K. Yalavarthy, “Deep neural network-based sinogram super-resolution and bandwidth enhancement for limited-data photoacoustic tomography,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 67, no. 12, pp. 2660–2673, 2020.
Y. Lou, W. Zhou, T. Matthews, C. Appleton, and M. Anastasio, “Generation of anatomically realistic numerical phantoms for photoacoustic and ultrasonic breast imaging,” Journal of biomedical optics, vol. 22, no. 4, p. 041015, 2017.
J. Kuntz, B. Flach, R. Kueres, W. Semmler, M. Kachelriess, and S. Bartling, “Constrained reconstructions for 4d intervention guidance,” Phys. Med. Biol., vol. 58, pp. 3283–3300, 2013.
Z. Wang, A. Bovik, H. Sheikh, and E. Simoncelli, “Image quality assessment: from error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, p. 600–612, Apr 2004.
Z. Wang, A. B. anbd H. Sheikh, and E. Simoncelli, “Quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, pp. 600–612, 2004.
A. Hauptmann, F. Lucka, M. Betcke, N. Huynh, J. Adler, B. Cox, P. Beard, S. Ourselin, and S. Arridge, “Model-based learning for accelerated, limited-view 3-d photoacoustic tomography,” IEEE Transactions on Medical Imaging, vol. 37, no. 6, p. 1382–1393, Jun 2018.