Observer-Based PD Controller for a Class of High Order Linear Unstable Delayed Systems

Authors

Keywords:

linear systems, delay systems, stability, Fuzzy Observability

Abstract

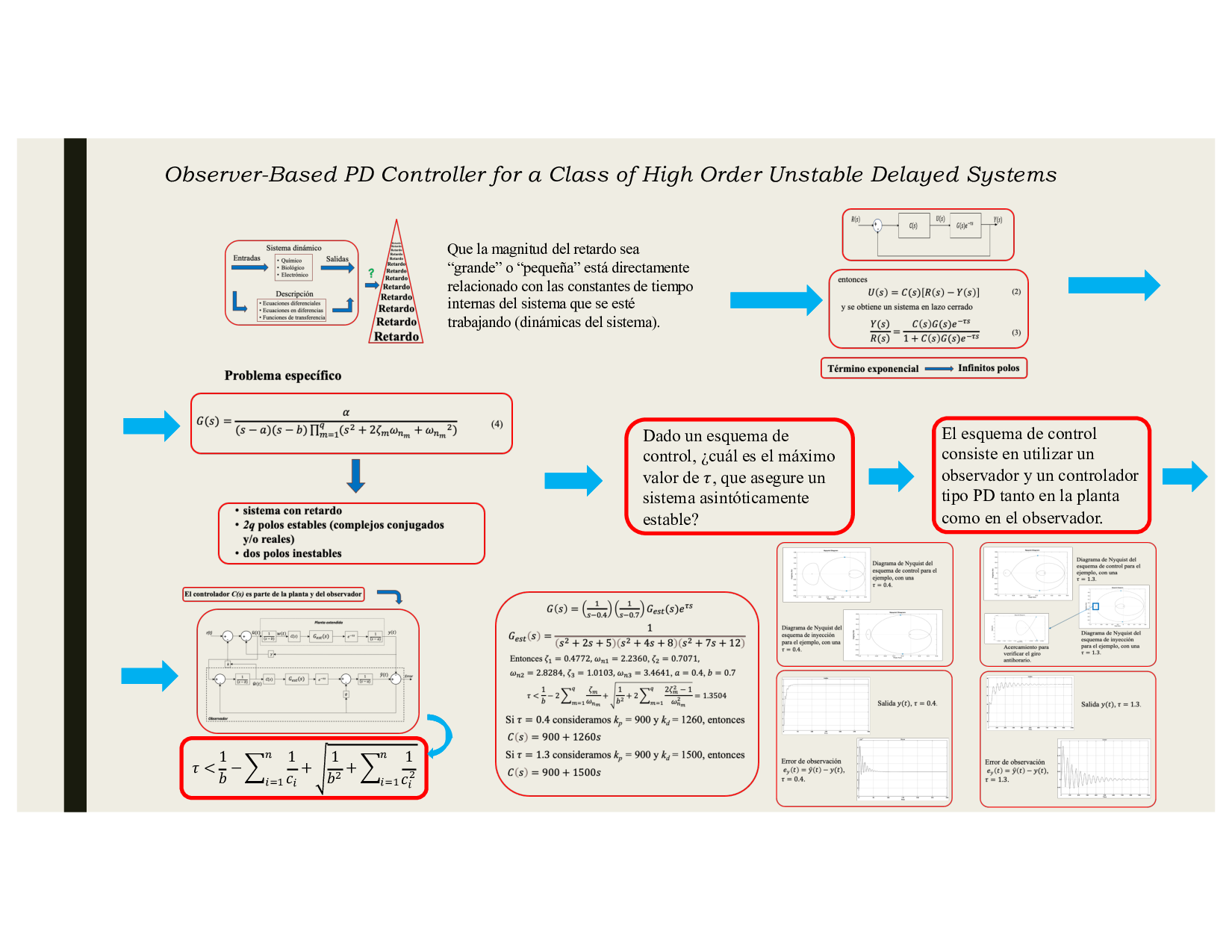
In this paper it is considered the stabilization and control of a class of high order linear systems that are subject to constant time delay at the input-output channel. In particular, systems with two unstable poles and any number of real or complex conjugate stable poles are studied. To improve the solutions existing in the literature, a new proposal for the solution of the considered problem is taken into account consisting in the design of an observer and a Proportional–Derivative PD controller to assure stable closed–loop performance, establishing by means of a frequency analysis necessary and sufficient conditions for the proposed control strategy. The proposal novelty is the inclusion of the PD control action in the observer that allows to estimate internal signals used in the solution. This configuration offers advantages in the time delay size that can be handled and on the control performance of the closed loop system. A practical design procedure is presented to determine the value of the controller gains. Numerical simulations examples are presented to show the operation of the proposal.

Downloads

Download data is not yet available.

Author Biographies

Gonzalo Duchén Sánchez, Instituto Politécnico Nacional

Gonzalo Duchén Sánchez nació en Sucre, Bolivia en 1962. Desde 1982 radica en México D.F. Estudió  Ingeniería Electrónica en la UAM Iztapalapa de 1982 a 1987 y realizó estudios de Doctorado en la misma universidad. Trabajó en la UAM Iztapalapa de 1987 a 1997 y a partir de entonces trabaja en la Sección de Estudios de Posgrado e Investigación (SEPI) de la ESIME, Unidad Culhuacan del IPN, Sus áreas de interés son los sistemas reconfigurables y sus aplicaciones al control, tratamiento de señales y criptografía. En su tiempo libre gusta leer y escuchar música.

Basilio del Muro Cuellar , Instituto Politecnico Nacional (Mexico)

Basilio del Muro Cuéllar es Ingeniero Industrial en Eléctrica por el Tecnológico de Morelia (1988),Maestro en Ciencias en Ingeniería Eléctrica con especialidad en Control Automático por el CINVESTAV1992) y Doctor en Ciencias para la Ingeniería en la especialidad de Control Automático por la Escuela Central de Nantes – Universidad de Nantes, Francia (1997). Desde 2005 se desempeña como profesor e investigador de tiempo completo en la Sección de Posgrado de la ESIME unidad Culhacán del Instituto Politécnico Nacional. Sus principales líneas de investigación incluyen el control de sistemas con retardo.

Juan Francisco Marquez Rubio, Instituto Politécnico Nacional

Juan Francisco Márquez Rubio recibió su Ph.D. en 2012 del Instituto Politécnico Nacional (IPN), ESIME Culhuacán en México. Actualmente es Profesor en el Instituto Politécnico Nacional, ESIME Culhuacán. Sus intereses de investigación incluyen problemas de observación, control y robustez además de métodos para el análisis de sistemas retardados.

Martín Velasco Villa, CINVESTAV-MEXICO

Martín Velasco-Villa realizó sus estudios de Maestría y Doctorado (1994) en el Cinvestav, México. Realizó además una estancia Postdoctoral en la Escuela Central de Nantes, Francia. Actualmente es profesor de tiempo completo en la Sección de Mecatrónica del Departamento de Ingeniería Eléctrica del Cinvestav. Sus áreas de interés son el análisis y control de sistemas lineales y no lineales con retardo y su aplicación en sistemas electromecánicos, en particular la robótica móvil.

Miguel Angel Hernández Pérez , Universidad Veracruzana

Miguel Ángel Hernández Pérez es egresado de la Universidad Autónoma del Estado de Hidalgo como ingeniero en Electrónica y Comunicaciones en 2009. Realizó sus estudios de Posgrado en el Instituto Politécnico Nacional donde obtuvo el grado de Maestro en Ciencias de Ingeniería en Microelectrónica en 2012 y el grado de Doctor en Comunicaciones y Electrónica en 2015. Actualmente es Profesor Investigador en el Instituto de Ingeniería de la Universidad Veracruzana. Sus temas de investigación se encuentran en el área de control lineal, análisis y modelado de sistemas con tiempo de retardo y sus aplicaciones, robótica móvil.

References

R. Sipahi, S. J. Nicolescu, C. T. Abdallah, W. Michiels, and K. Gu, “Stability and stabilization of systems with time delay,” IEEE Control Systems Magazine, vol. 31, pp. 38–65, 2011.

J. J. Loiseau, “Algebraic tools for the control and stabilization of timedelay systems,” in IFAC Workshop on Linear Time Delay Systems, vol. 31, pp. 187–201, 1998.

G. J. Silva, A. Datta, and S. P. Bhattacharyya, PID controllers for timedelay systems. Control engineering, Boston [u.a.]: Birkhäuser, 2005.

J. F. Marquez-Rubio, B. del Muro-Cuéllar, and J. Álvarez Ramírez, “Stabilization region of PD controller for unstable first order process with time delay,” International Journal of Control, Automation, and Systems, vol. 12, no. 2, pp. 265–273, 2014.

J. F. Márquez-Rubio, B. del Muro-Cuéllar, M. Velasco-Villa, and J. Ávarez Ramírez, “Control basado en un esquema observador para sistemas de primer orden con retardo,” Revista mexicana de ingeniería química, vol. 9, pp. 43 – 52, 04 2010.

C. Xiang, Q. G. Wang, X. Lu, L. A. Nguyen, and T. H. Lee, “Stabilization of second-order unstable delay processes by simple controllers,” Journal of process control, vol. 17, pp. 675–682, 2007.

S. C. Lee, Q. G. Wang, and C. Xiang, “Stabilization of all-pole unstable delay processes by simple controllers,” Journal of process control, vol. 20, pp. 235–239, 2010.

D. F. Novella-Rodríguez, B. del Muro-Cuéllar, and O. Sename, “Observer-based scheme for the control of high order systems with two unstable poles plus time delay,” Asia Pacific Journal of Chemical Engineering, vol. 9, pp. 167–180, 2014.

D. F. Novella-Rodríguez, B. del Muro Cuéllar, J. F. Márquez-Rubio, M. A. Hernández-Pérez, and M. Velasco-Villa, “PD—PID controller for delayed systems with two unstable poles: a frequency domain approach,” International Journal of Control, vol. 92, pp. 1196–1208, 2019.

C. D. Vázquez, J. F. Márquez, B. del Muro, D. Novella, M. A. Hernandez, and G. Duchen, “Observer-PI scheme for the stabilization and control of high order delayed systems with one or two unstable poles,” in 3rd IFAC Conference on Advances in Proportional-Integral- Derivative Control PID 2018, vol. 51, pp. 432–437, 2018.

M. A. Hernández-Pérez, B. del Muro-Cuéllar, and M. Velasco-Villa, “PID for the stabilization of high-order unstable delayed systems with possible complex conjugate poles,” Asia Pacific Journal of Chemical Engineering, vol. 10, no. 5, pp. 687–699, 2015.

G. Duchen, B. D. M. B, J. F. Márquez, M. A. Hernández, E. Ramírez, and C. Cruz, “Estabilización y control de sistemas de alto orden con retardo y dos polos inestables: esquema PD-observador,” in Memorias del Congreso Nacional de Control Automático 2019, pp. 291–296, AMCA, 2019.

H. Nyquist, “Regeneration theory,” The Bell System Technical Journal, vol. 11, pp. 126–147, 1932.

Downloads

Published

2021-09-13

How to Cite

Duchén Sánchez, G., del Muro Cuellar , B., Marquez Rubio, J. F., Velasco Villa, M., & Hernández Pérez , M. A. (2021). Observer-Based PD Controller for a Class of High Order Linear Unstable Delayed Systems. IEEE Latin America Transactions, 20(2), 291–300. Retrieved from https://latamt.ieeer9.org/index.php/transactions/article/view/5641

Issue

Vol. 20 No. 2 (2022): Ordinary Issue

Section

Articles