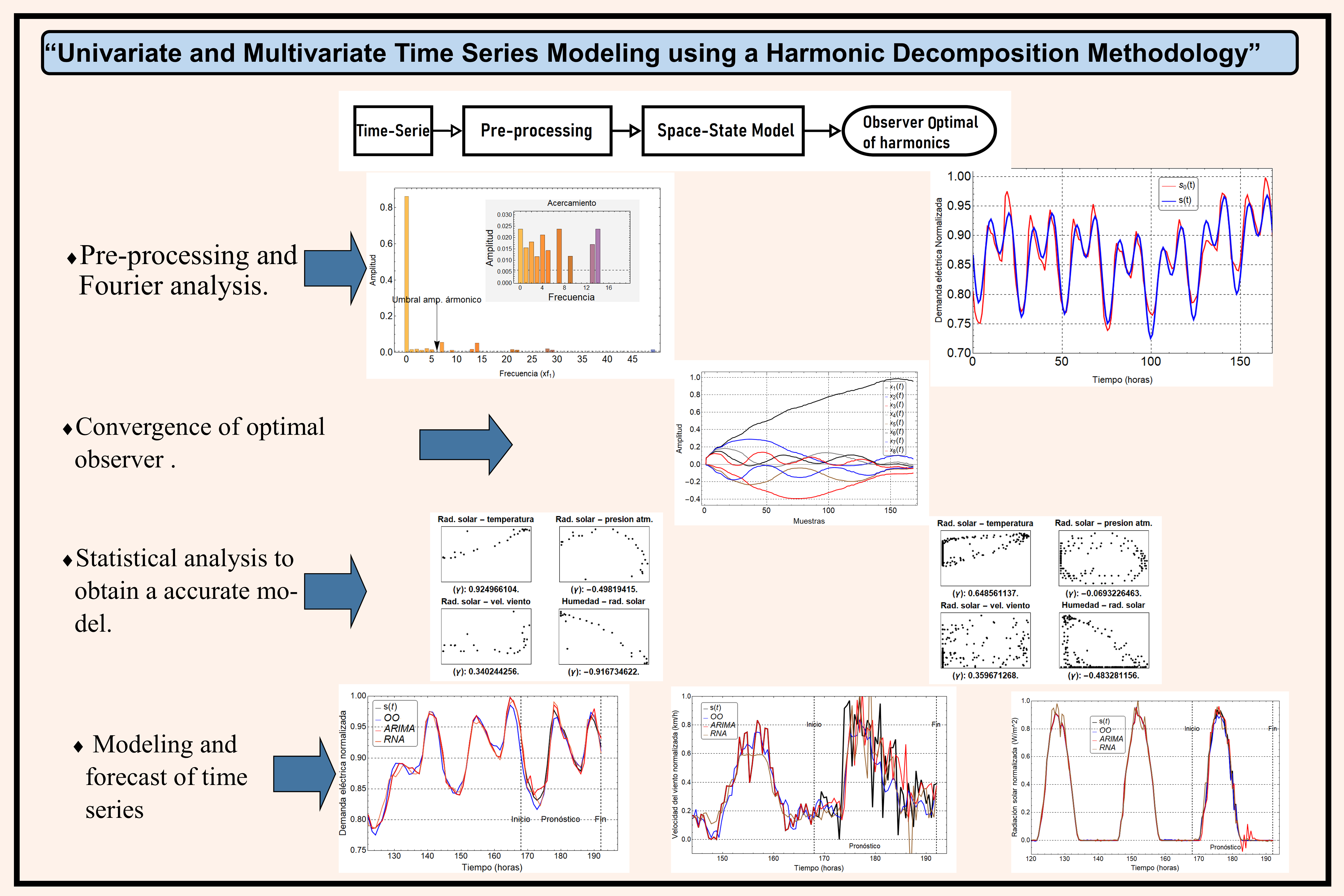
Univariate and Multivariate Time Series Modeling using a Harmonic Decomposition Methodology
Keywords:
Signal modeling, Time series, Optimal observer, Kalman-Bucy filter, Forecast, Fourier seriesAbstract
This paper contributes by developing an univariate and multivariate harmonic decomposition methodology to model time series.The models are stated in a state space representation derived from a Fourier series analysis to describe an arbitrary signal. The frequency values of the harmonic content are used to define state variables in order to describe a signal through a time-varying linear state space model, which serves to synthesize an optimal state observer (Kalman-Bucy filter). Once the observer converges and the states (harmonics) become constant, the observer model can be used to predict the signal, i.e., a time series forecasting can be performed.
The preocedure can be developed for the univariate or multivariate case of time series modeling, where in the last one, a statistical analysis is used to determine which variables should be taken into account to obtain a more accurate model. The proposed modeling approach is successfully applied for the modeling and forecast of the time series of electrical power demand and a wind/solar profile.
Downloads
References
D. E. Kirk, "Optimal Control Theory: An Introduction", 1st ed. Mineola,
New York: Dover Publications, Incs., 2004.
A. Isidori, "Nonlinear control systems", 1st ed. Springer-Verlag, London:
Springer Science and Business Media, 2013.
M. Falk and other, "A First Course on Time Series Analysis-Examples
whit SAS. Wurzburg", Alemania: University of Wuerzburg, 2012.
Y. Chen, B. Yang, J. Dong, and A. Abraham, "Time-series forecasting
using flexible neural tree model", Information Sciences, vol. 174, pp.
–235, 08 2005.
B. Box, G. Jenkins, G. Reinsel, and G. Ljung, "Time Series Analysis:
Forecasting and Control", vol. 68, 2016.
B. M. del Brio and A. S. Molina, "Redes neuronales y sistemas borrosos",
rd ed. Madrid, Espana: ALFAOMEGA GPO ED, 2015.
E. N. Sanchez, A. Y. Alanis, and J. Rico, "Electric load demand prediction using neural network trained by Kalman filtering", in 2004 IEEE
International Joint Conference on Neural Networks, vol. 4, Budapest,
Hungary, pp. 2771–2775. july 2004.
R. L. Farias, J. J. Flores, and V. Puig, "Qualitative and quantitative multimodel forecasting with nonlinear noise filter applied to water demand",
in 2015 IEEE International Autumn Meeting on Power, Electronics and
Computing (ROPEC), Ixtapa, Mexico, pp. 1–6, nov 2015.
C. Chatfield and D. Prothero, "Box-jenkins seasonal forecasting: problems in a case-study", Journal of the Royal Statistical Society: Series A
(General), vol. 136, no. 3, pp. 295–315, 1973.
O. D. Anderson, "The box-jenkins approach to time series analysis",
RAIRO - Operations Research, vol. 11, no. 1, pp. 3–29, 1977.
K. H. A. McLeod, "Time Series Modelling of Water Resources and Environmental Systems", Volume 45. P.O. Box 211, 1000, AE Amsterdam,
The Netherland: Elsevier Science, 1994.
E. de la Vega, J. J. Flores, and M. Graff, "k-nearest-neighbor by
differential evolution for time series forecasting", in Nature-Inspired
Computation and Machine Learning, A. Gelbukh, F. C. Espinoza, and
S. N. Galicia-Haro, Eds., vol. 8857. Switzerland: Springer, pp.
–60, 2014.
R. Kalman and R. Bucy, in Journal of Basic Engineering, vol. 83, no. 1, pp. 95–108, march 1961.
D. Simon, "Kalman filtering with state constraints: a survey of linear
and nonlinear algorithms", IET Control Theory & Applications, vol. 4,
no. 8, pp. 1303–1318, 2010.
F. Ornelas-Tellez, J. J. Rico-Melgoza, R. Morfin-Magana, and S. Ramos-Paz, "Optimal dynamic harmonic extraction and suppression in power
conditioning applications", IEEE Transactions on Industrial Electronics,
vol. 67, no. 9, pp. 7909–7918, 2020.
A. A. Garibo-Morante and F. Ornelas-Tellez, "Modeling and forecast of
time series by using a harmonic decomposition approach", in 2019 IEEE
International Autumn Meeting on Power, Electronics and Computing
(ROPEC), Ixtapa, Mexico, pp. 1–6, 2019.
E. N. Lorenz, "Deterministic nonperiodic flow", Journal of atmospheric
sciences, vol. 20, no. 2, pp. 130–141, 1963.
G. Layek, "An introduction to dynamical systems and chaos", Springer,
India, 2015.
J. C. Knievel, D. A. Ahijevych, and K. W. Manning, “Using temporal
modes of rainfall to evaluate the performance of a numerical weather
prediction model", Monthly weather review, vol. 132, no. 12, pp. 2995–
, 2004.
A. Zygmund, "Trigonometric series", 3rd ed. New York, NY, USA:
Cambridge university press, vol. 1, 2002.
G. P. Tolstov, "Fourier Series", 1st ed. Englewood Cliffs, NJ, USA:
Prentice-Hall, Inc., 1962.
B. Friedland, "Control System Design: An Introduction to State-Space
Methods", kindle ed. New York, NY, USA: McGraw-Hill, 1986.
R. F. Stengel, "Optimal Control and Estimation", 2nd ed. New York,
NY, USA: Robert F. Stengel, 1994.
J. De Leeuw, "Models and methods for the analysis of correlation
coefficients", Journal of Econometrics, vol. 22, no. 1, pp. 113–137, 1983.
A. G. Asuero, A. Sayago, and A. G. Gonzalez, "The correlation coefficient: An overview", Critical Reviews in Analytical Chemistry,
vol. 36, no. 1, pp. 41–59, 2006.
P. Cohen, S. G. West, and L. S. Aiken, "Applied multiple regression/correlation analysis for the behavioral sciences", 3rd ed. Mahwah,
New Jersey, London: Lawrence Erlbaum Associates, 2014.
J. A. Mauricio, "Introduccion al Analisis de Series Temporales", 1st ed.,
Universidad Complutense de Madrid, Espana, 2013.
J. Tayman and D. A. Swanson, "On the validity of mape as a measure of
population forecast accuracy", Population Research and Policy Review,
vol. 18, no. 4, pp. 299–322, 1999.