An Investigation into Many-objective Optimization Problems: A Case Study of the Dial-a-Ride Problem
Keywords:
Many-objective optimization, dial-a-ride problem, multi-objective evolutionary algorithms, combinatorial optimizationAbstract
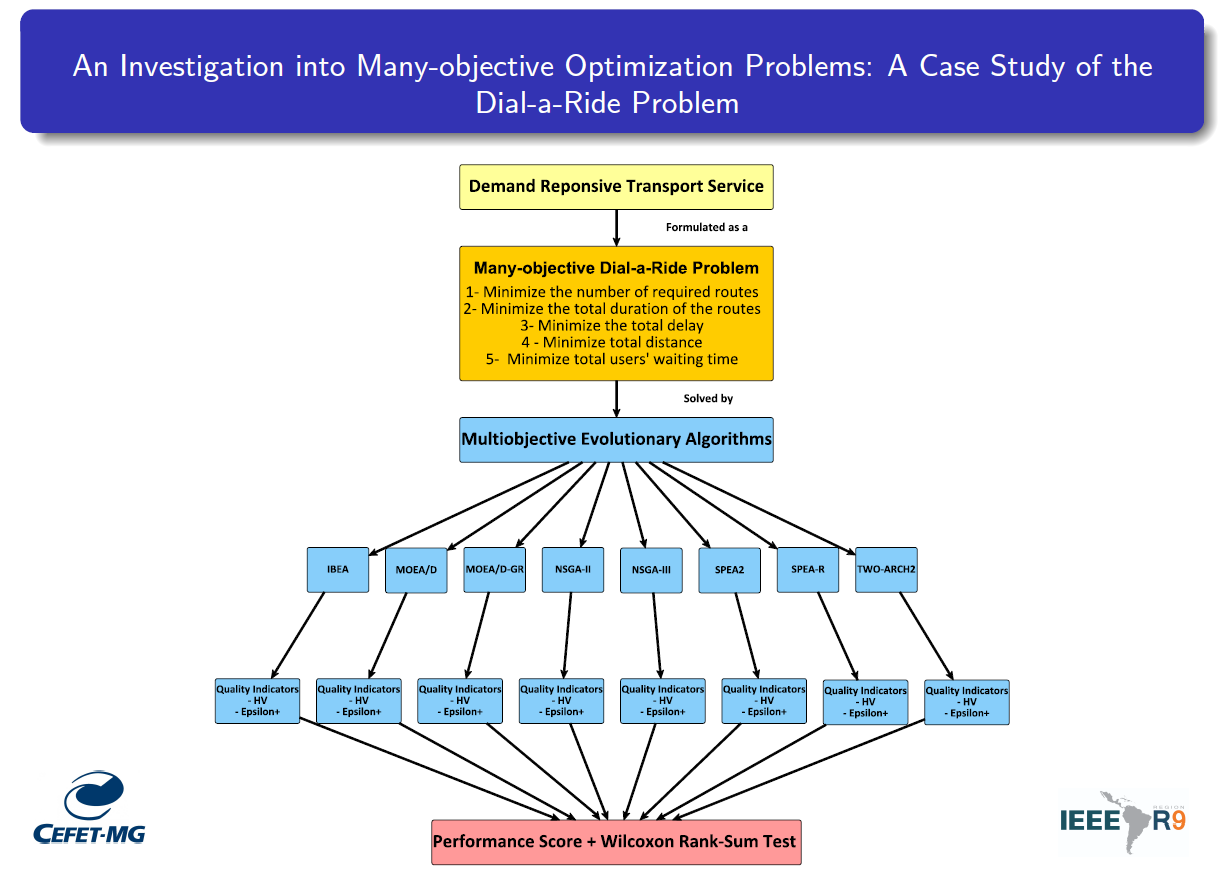
Multi-objective optimization problems with more than three objectives are commonly referred to as many-objective optimization problems. Usually, this class of problem brings new and complex challenges to the current optimization methods, mainly maintaining the right balance between convergence and diversity. During the last years, various approaches have been proposed to solve many-objective problems. However, most existing experimental comparative studies are restricted to continuous problems. Few studies have encompassed the most recently proposed state-of-the-art approaches and made an experimental comparison applied to combinatorial optimization problems. Aiming to fill this gap, this paper presents a comparative analysis with eight algorithms covering various categories to solve a many-objective Dial-a-Ride problem. The results show that different observations can be made about the algorithms' behavior when using different test sets. Also, algorithms originally proposed to deal with problems with up to three objectives have overcome recently proposed ones.
Downloads
References
J. Mageean and J. D. Nelson, “The evaluation of demand responsive
transport services in europe,” Journal of Transport Geography, vol. 11,
no. 4, pp. 255–270, 2003.
G. Ambrosino, J. Nelson, and M. Romanazzo, Demand responsive
transport services: Towards the flexible mobility agency. ENEA, Italian
National Agency for New Technologies, Energy and the Environment,
J.-F. Cordeau and G. Laporte, “The dial-a-ride problem: models and
algorithms,” Annals of Operations Research, vol. 153, no. 1, pp. 29–46,
——, “A tabu search heuristic for the static multi-vehicle dial-a-ride
problem,” Transportation Research Part B: Methodological, vol. 37,
no. 6, pp. 579–594, 2003.
J.-F. Cordeau, “A branch-and-cut algorithm for the dial-a-ride problem,”
Operations Research, vol. 54, no. 3, pp. 573–586, 2006.
Y. Molenbruch, K. Braekers, and A. Caris, “Typology and literature
review for dial-a-ride problems,” Annals of Operations Research, vol.
, no. 1-2, pp. 295–325, 2017.
S. C. Ho, W. Szeto, Y.-H. Kuo, J. M. Leung, M. Petering, and T. W.
Tou, “A survey of dial-a-ride problems: Literature review and recent
developments,” Transportation Research Part B: Methodological, 2018.
U. Ritzinger, J. Puchinger, and R. F. Hartl, “Dynamic programming
based metaheuristics for the dial-a-ride problem,” Annals of Operations
Research, vol. 236, no. 2, pp. 341–358, 2016.
R. Chevrier, A. Liefooghe, L. Jourdan, and C. Dhaenens, “Solving a
dial-a-ride problem with a hybrid evolutionary multi-objective approach:
Application to demand responsive transport,” Applied Soft Computing,
vol. 12, no. 4, pp. 1247–1258, 2012.
B. Rekiek, A. Delchambre, and H. A. Saleh, “Handicapped person
transportation: An application of the grouping genetic algorithm,” Engineering
Applications of Artificial Intelligence, vol. 19, no. 5, pp. 511–
, 2006.
T. Garaix, C. Artigues, D. Feillet, and D. Josselin, “Optimization of
occupancy rate in dial-a-ride problems via linear fractional column
generation,” Computers & Operations Research, vol. 38, no. 10, pp.
–1442, 2011.
S. N. Parragh, J. Pinho de Sousa, and B. Almada-Lobo, “The dial-a-ride
problem with split requests and profits,” Transportation Science, vol. 49,
no. 2, pp. 311–334, 2014.
A. Lim, Z. Zhang, and H. Qin, “Pickup and delivery service with
manpower planning in hong kong public hospitals,” Transportation Science, vol. 51, no. 2, pp. 688–705, 2016.
R. M. Jorgensen, J. Larsen, and K. B. Bergvinsdottir, “Solving the diala-
ride problem using genetic algorithms,” Journal of the operational
research society, vol. 58, no. 10, pp. 1321–1331, 2007.
D. Kirchler and R. W. Calvo, “A granular tabu search algorithm for the
dial-a-ride problem,” Transportation Research Part B: Methodological,
vol. 56, pp. 120–135, 2013.
M. Schilde, K. F. Doerner, and R. F. Hartl, “Integrating stochastic timedependent
travel speed in solution methods for the dynamic dial-a-ride
problem,” European journal of operational research, vol. 238, no. 1, pp.
–30, 2014.
R. Chevrier, A. Liefooghe, L. Jourdan, and C. Dhaenens, “On optimizing
a demand responsive transport with an evolutionary multi-objective
approach,” in Intelligent Transportation Systems (ITSC), 2010 13th
International IEEE Conference on. IEEE, 2010, pp. 575–580.
J. Paquette, J.-F. Cordeau, G. Laporte, and M. M. Pascoal, “Combining
multicriteria analysis and tabu search for dial-a-ride problems,” Transportation Research Part B: Methodological, vol. 52, pp. 1–16, 2013.
Y. Molenbruch, K. Braekers, A. Caris, and G. V. Berghe, “Multidirectional
local search for a bi-objective dial-a-ride problem in patient
transportation,” Computers & Operations Research, vol. 77, pp. 58–71,
R. J. S. Viana, A. G. Santos, F. V. C. Martins, and E. F.
Wanner, “Optimization of a demand responsive transport service
using multi-objective evolutionary algorithms,” in Proceedings of the
Genetic and Evolutionary Computation Conference Companion,
ser. GECCO ’19. New York, NY, USA: Association for
Computing Machinery, 2019, p. 2064–2067. [Online]. Available:
https://doi.org/10.1145/3319619.3328528
R. S. Mendes, D. S. Miranda, E. F. Wanner, J. F. M. Sarubbi, and F. V. C.
Martins, “Multiobjective approach to the vehicle routing problem with
demand responsive transport,” in 2016 IEEE Congress on Evolutionary
Computation (CEC), 2016, pp. 3761–3768.
R. Mendes, E. Wanner, F. Martins, and J. Sarubbi, “Dimensionality
reduction approach for many-objective vehicle routing problem with demand
responsive transport,” in International Conference on Evolutionary
Multi-Criterion Optimization. Springer, 2017, pp. 438–452.
R. S. Mendes, V. Lush, E. F. Wanner, F. V. Martins, J. F.
Sarubbi, and K. Deb, “Online clustering reduction based on
parametric and non-parametric correlation for a many-objective vehicle
routing problem with demand responsive transport,” Expert Systems
with Applications, vol. 170, p. 114467, 2021. [Online]. Available:
http://www.sciencedirect.com/science/article/pii/S0957417420311180
A. A. Anwar and I. Younas, “Optimization of many objective pickup and
delivery problem with delay time of vehicle using memetic decomposition
based evolutionary algorithm,” International Journal on Artificial
Intelligence Tools, vol. 29, no. 01, 2020.
H. Zhao, C. Zhang, J. Ning, B. Zhang, P. Sun, and Y. Feng, “A comparative
study of the evolutionary many-objective algorithms,” Progress
in Artificial Intelligence, vol. 8, no. 1, pp. 15–43, 2019.
B. Li, J. Li, K. Tang, and X. Yao, “Many-objective evolutionary
algorithms: A survey,” ACM Comput. Surv., vol. 48, no. 1, Sep. 2015.
[Online]. Available: https://doi.org/10.1145/2792984
R. J. D. S. VIANA, “Abordagens heur´ısticas para otimizac¸ ˜ao de um
servic¸o de transporte reativo a demanda,” Master’s thesis, Programa de
P´os-Graduac¸ ˜ao em Ciˆencia da Computac¸ ˜ao, Universidade Federal de
Vic¸osa, 2016.
C. C. Coello, G. B. Lamont, and D. A. Van Veldhuizen, Evolutionary
algorithms for solving multi-objective problems. Springer, 2007.
V. Pareto, “Cours deconomie, vol. I and II, f,” Rouge, Lausanne, 1896.
K. Deb, Multi-objective optimization using evolutionary algorithms.
John Wiley & Sons, 2001, vol. 16.
A. Abraham and L. Jain, Evolutionary multiobjective optimization.
Springer, 2005.
K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist
multiobjective genetic algorithm: Nsga-ii,” Evolutionary Computation,
IEEE Transactions on, vol. 6, no. 2, pp. 182–197, 2002.
E. Zitzler, M. Laumanns, L. Thiele, E. Zitzler, E. Zitzler, L. Thiele,
and L. Thiele, “SPEA2: Improving the strength pareto evolutionary algorithm,”
Eidgen¨ossische Technische Hochschule Z¨urich (ETH), Institut
f¨ur Technische Informatik und Kommunikationsnetze (TIK), Tech. Rep.,
Q. Zhang and H. Li, “Moea/d: A multiobjective evolutionary algorithm
based on decomposition,” IEEE Transactions on evolutionary computation,
vol. 11, no. 6, pp. 712–731, 2007.
Z. Wang, Q. Zhang, M. Gong, and A. Zhou, “A replacement strategy for
balancing convergence and diversity in moea/d,” in 2014 IEEE Congress
on Evolutionary Computation (CEC). IEEE, 2014, pp. 2132–2139.
E. Zitzler and S. K¨unzli, “Indicator-based selection in multiobjective
search,” in Parallel Problem Solving from Nature-PPSN VIII. Springer,
, pp. 832–842.
K. DEB and H. JAIN, “An evolutionary many-objective optimization
algorithm using reference-point-based nondominated sorting approach,
part i: Solving problems with box constraints,” IEEE transactions on
evolutionary computation, vol. 18, no. 4, pp. 577–601, 2014.
S. Jiang and S. Yang, “A strength pareto evolutionary algorithm based on
reference direction for multiobjective and many-objective optimization,”
IEEE Transactions on Evolutionary Computation, vol. 21, no. 3, pp.
–346, 2017.
H. Wang, L. Jiao, and X. Yao, “Two arch2: An improved two-archive
algorithm for many-objective optimization,” IEEE Transactions on Evolutionary
Computation, vol. 19, no. 4, pp. 524–541, 2015.
J. D. Knowles, L. Thiele, and E. Zitzler, “A tutorial on the performance
assessment of stochastic multiobjective optimizers,” TIK-Report, vol.
, 2006.
E. Zitzler and L. Thiele, “Multiobjective optimization using evolutionary
algorithms - a comparative case study,” in Parallel problem solving from
nature - PPSN V. Springer, 1998, pp. 292–301.
E. Zitzler, L. Thiele, M. Laumanns, C. M. Fonseca, and V. G. Da Fonseca,
“Performance assessment of multiobjective optimizers: An analysis
and review,” Evolutionary Computation, IEEE Transactions on, vol. 7,
no. 2, pp. 117–132, 2003.
C. M. Fonseca, J. D. Knowles, L. Thiele, and E. Zitzler, “A tutorial on
the performance assessment of stochastic multiobjective optimizers,” in
Third International Conference on Evolutionary Multi-Criterion Optimization
(EMO 2005), vol. 216, 2005, p. 240.
J. Bader and E. Zitzler, “Hype: An algorithm for fast hypervolume-based
many-objective optimization,” Evolutionary computation, vol. 19, no. 1,
pp. 45–76, 2011.
I. Das and J. E. Dennis, “Normal-boundary intersection: A new method
for generating the pareto surface in nonlinear multicriteria optimization
problems,” SIAM journal on optimization, vol. 8, no. 3, pp. 631–657,
R. Tanabe, H. Ishibuchi, and A. Oyama, “Benchmarking multi- and
many-objective evolutionary algorithms under two optimization scenarios,”
IEEE Access, vol. 5, pp. 19 597–19 619, 2017.
L. C. Bezerra, M. L´opez-Ib´a˜nez, and T. St¨utzle, “A large-scale experimental
evaluation of high-performing multi-and many-objective evolutionary
algorithms,” Evolutionary computation, vol. 26, no. 4, pp. 621–
, 2018.