An Algorithm to Belief Revision and to Verify Consistency of a Knowledge Base
Keywords:
Belief revision, Propositional inference, Knowledge base, Consistency, Satisfiability problem.Abstract
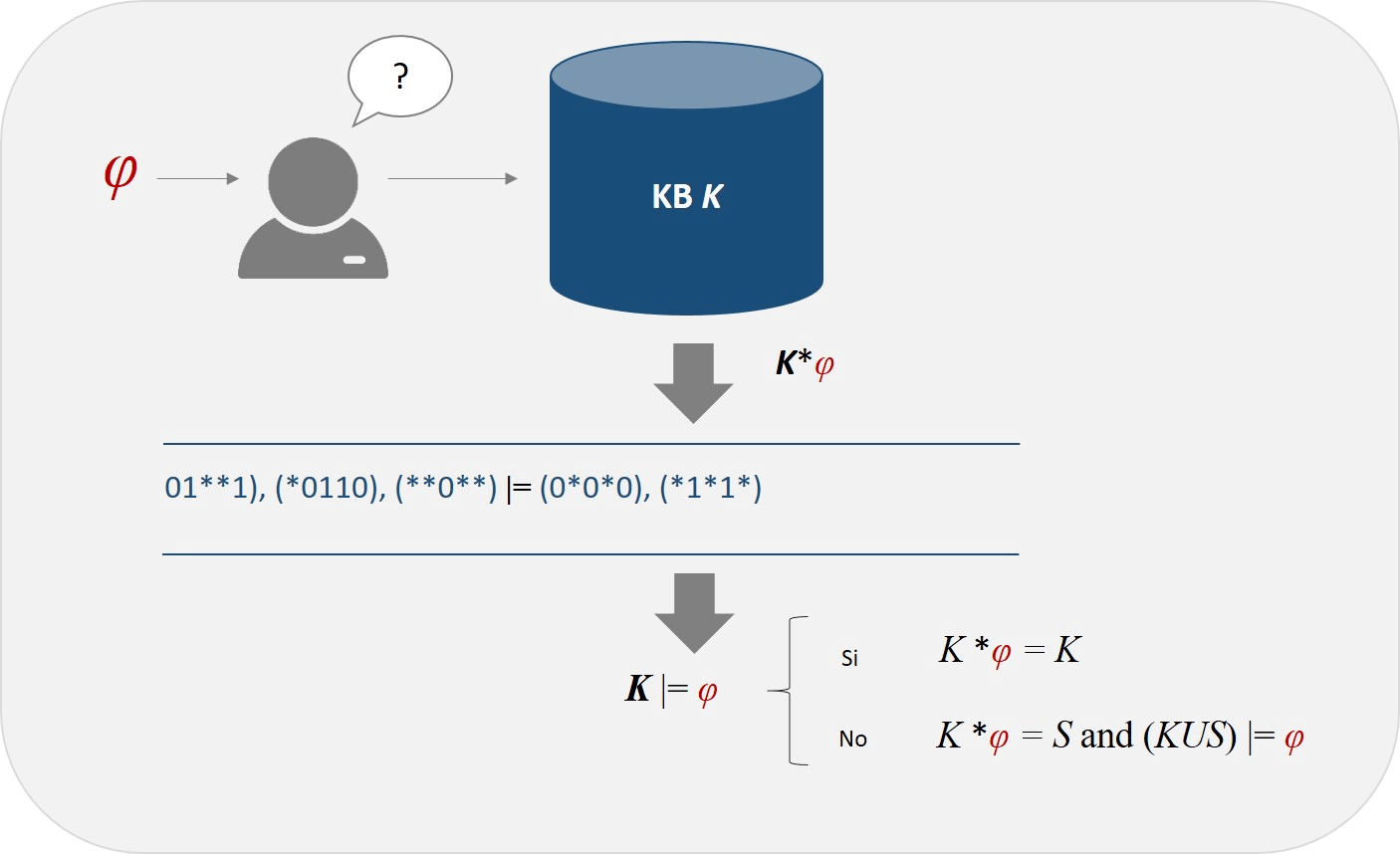
The belief revision process involves several problems considered hard. One of the crucial problems is how to represent to the knowledge base K to consider, as well as how to represent and to add new information φ, which may even be contradictory to the knowledge base. In this work, both the knowledge base and the new information are in conjunctive normal form. Each clause of a conjunctive normal form is encoded by a string consisting of: 0, 1, *, representing the falsifying assignments of the clause. To use the falsifying assignments of the clauses allows to perform efficiently different logical operators among conjunctive forms. Our belief revision process (K * φ) between conjunctive forms is based on solving first the propositional inference, i.e. K |= φ. Based on to count falsifying assignments represented by tertiary chains, an algorithmic proposal is made that allows to determine in a practical way, when (K È ( K * φ)) is inconsistent. Finally, the time-complexity analysis of our algorithmic proposal is carried out.
Downloads
References
M. Aiguier, J. Atif, I. Bloch, and C., Hudelot, “Belief revision, minimal change and relaxation: a general framework based on satisfaction systems, and applications to description logics”, Artificial Intelligence, 256, pp. 160–180, 2018.
C. Alchourrón, P. Gärdenfors, and D. Makinson, “On the logic of theory change: Partial meet contraction and revision functions”, Journal of Symbolic Logic, 50, pp. 510–530, 1985.
Anfrix. De las conductas indecorosas en la mesa de mi señor. Recuperado de: https://www.anfrix.com/2006/01/codex romanoff-ii-los-modales-en-la-mesa-medieval/, 20 de abril de 2020.
C. Beierle, C. Eichhorn, and G. Kern-Isberner, “On transformations and normal forms of conditional knowledge bases”, Springer International Publishing AG, 1, pp. 488–494, 2017.
T. Caridroit, S. Konieczny, and P. Marquis, “Contraction in propositional logic”, International Journal of Approximate Reasoning, 80, pp. 428–442, 2017.
N. Creignou, O. Papini, R. Pichler, and S. Woltran, “Belief Update within Propositional Fragments”, Journal of Artificial Intelligence Research, 61, pp. 807–834, 2018.
N. Creignou, O. Papini, R. Pichler, and S. Woltran, ”Belief revision within fragments of propositional logic”, In Proceedings of the Thirteenth International Conference on Principles of Knowledge Representation and Reasoning, KR’12, p.p. 126–136. AAAI Press. ISBN 978-1-57735-560-1. 2014.
E. Cresto, “Revisión de creencias y racionalidad”, Cuadernos CIMBAGE, 5, pp. 133–156, 2002.
G. De Ita , J.R. Marcial, J.A. Hernández, P. Bello, Lógica proposicional y de predicados, En Conocimiento y razonamiento computacional, Academia Mexicana de Computación, A.C., (2019).
O. Doubois, “Counting the number of solutions for instances of satisfiability”, Theoretical Computer Science, 81, pp. 49–64, 1991.
E. Fermé, “Revisión de creencias”, Revista Iberoamericana de Inteligencia Artificial, 11(34), pp. 17–39, 2007.
J. Gallier, Logic for Computer Science: Foundations of Automatic Theorem Proving, Dover Publicatios, Philadelphia, USA, second edition, pp. 28-141. 2015.
P. Gärdenfors, Belief revisión: An introduction, Great Britain: Cambridge University Press, Ed. Cambridge, 29, pp. 1-28, 1992.
H. Katsuno, and A. O. Mendelzon, “Propositional knowledge base revision and minimal change”, Artificial Intelligence, 52(3), pp. 263–294, 1991.
R. Khardon, and D. Roth, “Reasoning with models”, Artificial Intelligence, 87, pp. 187–213, 1996.
P. Liberatore, “Revision by history”, Journal Artif. Intell. Res., 52:287–329, doi:10.1613/jair.4608. URL”https://doi.org/10.1613/jair.4608”, 2015.
P. Liberatore, M. Schaerf, “The complexity of model checking for Belief Revision and Update”, In AAAI-96 Proceedings, pp. 556 – 561, 1996.
S. Luan, G. Dai, and L. Magnani, “An approximate approach to belief revision”, Logic Journal of the IGPL, 2, 2012.
C. Pons, R. Rosenfeld, and C. Smith. Lógica para Informática. Editorial de la Universidad Nacional de La Plata (EDULP), 2017.
H. Velázquez, “Lógica deóntica: breve panorama de la cuestión”, Cuadrante Phi Revista de estudiantes de filosofía 28, pp. 1-24, 2015.
MA. Williams, “Applications of belief revision”, In Freitag B., Decker H., Kifer M., Voronkov (eds), Transactions and Change in Logic Databases, Lecture Notes in Comp. Sc. Vol 1472, Springer, 1997, https://doi.org/10.1007/BFb0055503
F. Zacarias and G. De Ita, “A Model-Based Algorithm for Propositional Belief Revision”, Latin America Transactions, IEEE. 13, pp. 1055-1060, 10.1109/TLA.2015.7106357, 2015.
H. R. Zuleta, “Lógica deóntica y verdad”, Análisis filosófico XXVI, 1, pp. 115-133, 2006.