Ultra-High-Speed Transmission Line Differential Protection using an Error Index of Bergeron Equation
Keywords:
bergeron equation, differential protection, error index, synchronized measurements, transmission lineAbstract
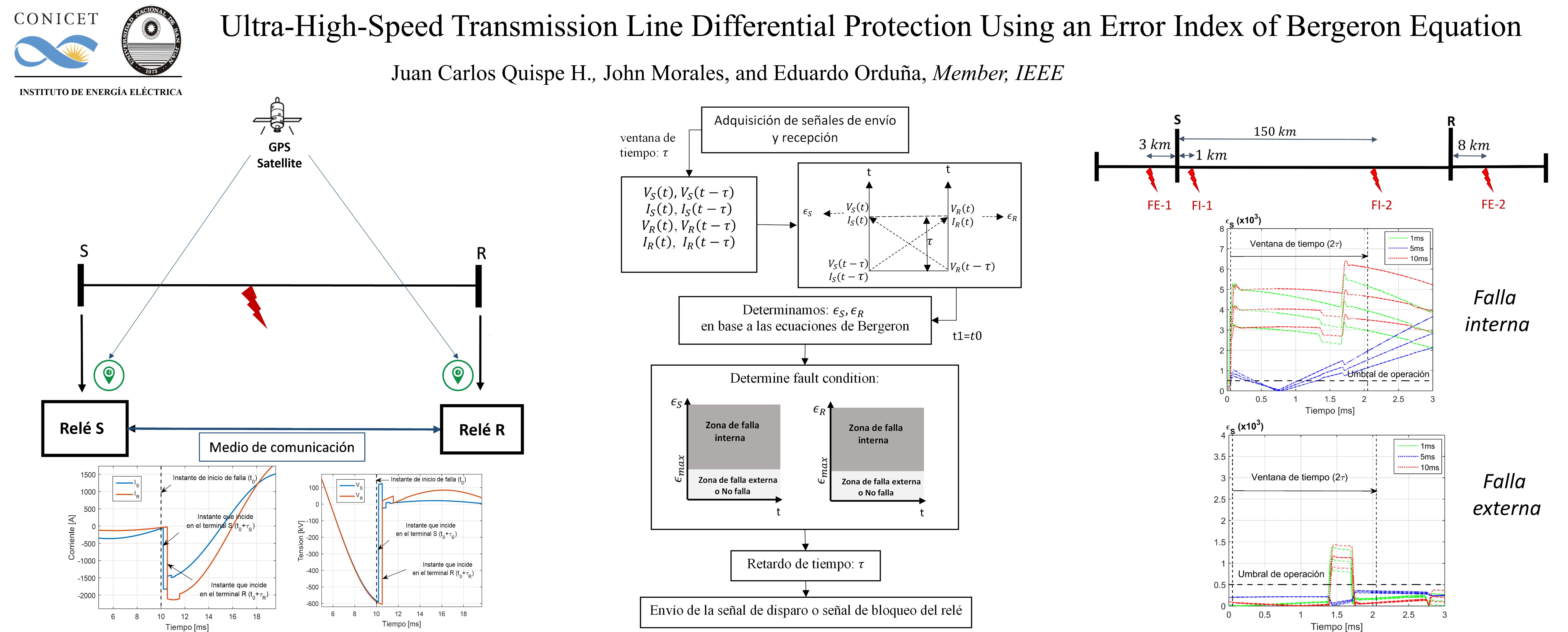
The Ultra-high-speed and simplicity of protection schemes have been a subject of study in recent years. Therefore this document develop a differential protection method in transmission lines using voltage and current traveling waves signals, where the transmission lines are modeled through distributed parameters and expressed by telegraph's equations which is solved using Bergeron's equations, these equations depend on instantaneous signals and historical components. Using an error index that compares the voltage and current signals from the line ends, the fault is detected. Furthermore, signals with synchronized measurements with the same time stamp are considered. This method uses simple criteria and fast operation time, because it uses algebraic operations and a time window between 1 and 2 ms. A power system is modeled on ATPDraw and many faults cases are simulated; several conditions such as inception angle from voltage signal, fault resistance, fault distance and internal/external faults are considered. In the case of three-phase systems, the use of Clarke's modal decomposition is proposed. Good results in the operation are obtained and comparing with traditional algorithms this method presents low operating times.
Downloads
References
S. S. K. Johns AT, “Digital protection for power system ,” P. P. Ltd., Ed. IEEE power series 15 , 1995.
W. Rebizant., “Digital signal processing in power system protection and control, signals and communication technology.,” Springer-Verlag, Ed. 2011.
H. A. Darwish, A. M. I. Taalab, and E. S. Ahmed, “Investigation of power differential concept for line protection,” IEEE Trans. Power Deliv., vol. 20, no. 2 I, pp. 617–624, Apr. 2005, doi: 10.1109/TPWRD.2004.838516.
E. O. Schweitzer, B. Kasztenny, A. Guzmán, V. Skendzic, and M. V Mynam, “Speed of line protection - can we break free of phasor limitations?,” in 2015 68th Annual Conference for Protective Relay Engineers, 2015, pp. 448–461, doi: 10.1109/CPRE.2015.7102184.
W. E. Vargas and H. C. Juan Quispe, “Economic Benefit and Improve of Stability in the Power System through the Ultra-High Speed Fault Clearing in Transmission Lines,” 2018, doi: 10.1109/INTERCON.2018.8526425.
Y. Hu, D. Chen, X. Yin, Z. Zhang, and Y. Chen, “The theory and application of differential protection based on instantaneous values,” in IEEE/PES Transmission and Distribution Conference and Exhibition, 2002, vol. 1, pp. 130–135 vol.1, doi: 10.1109/TDC.2002.1178272.
M. Wen, D. Chen, and X. Yin, “Instantaneous Value and Equal Transfer Processes-Based Current Differential Protection for Long Transmission Lines,” IEEE Trans. Power Deliv., vol. 27, no. 1, pp. 289–299, 2012, doi: 10.1109/TPWRD.2011.2170438.
H. w. Dommel and J. M. Michels, “HIGH SPEED RELAYING USING TRAVELING WAVE TRANSIENT ANALYSIS.,” IEEE PES (Power Eng Soc) Winter Meet, Prepr, 1978, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-84954451629&partnerID=40&md5=acf5556a82c75a8b0c9df960d16efde9.
J. B. T.Takagi U. Katsuhiko and T. Sakaguchi, “Fault Protection Based on Travelling Wave Theory - Part I Theory,” IEEE PES Summer Meeting. .
J. B. T.Takagi U. Katsuhiko and T. Sakaguchi, “Fault Protection Based on Travelling Wave Theory - Part II Sensitivity Analysis and Laboratory Test ,” IEEE PES Summer Meeting. .
T. Y. Yoshiakira Akimoto Hiroshi Hosakawa, Toshiaki Sakaguchi, Takashi Yoshida And Syozo Nishida, “Fault Protection Based on Travelling Wave Theory (Part I-Theory),” Electr. Eng. Japan, vol. Vol. 98, N, 1978.
H. H. T. Y. Yoshiakira Akimoto Toshiaki Sakaguchi, Takashi Yoshida, and A. S. Nishida, “Fault Protection Based on Travelling Wave Theory (Part II-Feasibility Study).”
B. Su, X. Dong, and Y. Sun, “A new traveling wave differential relay for series compensated EHV transmission line,” in 2004 Eighth IEE International Conference on Developments in Power System Protection, 2004, vol. 2, pp. 420-423 Vol.2, doi: 10.1049/cp:20040151.
S. Hasheminejad, S. G. Seifossadat, M. Razaz, and M. Joorabian, “Ultra-high-speed protection of transmission lines using traveling wave theory,” Electr. Power Syst. Res., vol. 132, pp. 94–103, 2016, doi: https://doi.org/10.1016/j.epsr.2015.11.014.
H. HengXu, Y. Yang, Y. RuiPeng, Z. Q. Bo, and C. Bo, “Novel scheme of travelling wave based differential protection for bipolar HVDC transmission lines,” in 2010 International Conference on Power System Technology, 2010, pp. 1–6, doi: 10.1109/POWERCON.2010.5666376.
L. Tang, X. Dong, S. Luo, S. Shi, and B. Wang, “A New Differential Protection of Transmission Line Based on Equivalent Travelling Wave,” IEEE Trans. Power Deliv., vol. 32, no. 3, pp. 1359–1369, 2017, doi: 10.1109/TPWRD.2016.2568206.
W. Chi-Kong, L. Chi-Wai, L. Kuok-Cheong, L. Chu-San, and H. Ying-Duo, “Novel wavelet approach to current differential pilot relay protection,” IEEE Trans. Power Deliv., vol. 18, no. 1, pp. 20–25, 2003, doi: 10.1109/TPWRD.2002.803733.
P. Jafarian and M. Sanaye-Pasand, “A Traveling-Wave-Based Protection Technique Using Wavelet/PCA Analysis,” IEEE Trans. Power Deliv., vol. 25, no. 2, pp. 588–599, 2010, doi: 10.1109/TPWRD.2009.2037819.
Q. H. Wu, J. F. Zhang, and D. J. Zhang, “Ultra-high-speed directional protection of transmission lines using mathematical morphology,” IEEE Trans. Power Deliv., vol. 18, no. 4, pp. 1127–1133, Oct. 2003, doi: 10.1109/TPWRD.2003.817513.
B. Li, W. Chang, J. He, and Z. Bo, “Special Problems in Current Differential Protection Based on Bergeron Model,” in 2009 Asia-Pacific Power and Energy Engineering Conference, 2009, pp. 1–4, doi: 10.1109/APPEEC.2009.4918778.
J. C. H. Quispe and E. Orduna, “A New Method to Fault Localization in Long Transmission Lines Considering Synchronized Sampling,” 2018, doi: 10.1109/INTERCON.2018.8526447.
“C37.241-2017 - C37.241-2017 - IEEE Guide for Application of Optical Instrument Transformers for Protective Relaying - IEEE Standard.” https://ieeexplore.ieee.org/document/8307291 (accessed Oct. 19, 2020).
U. of Pennsylvania, “D’alembert’s solution of the wave equation (spring 2016).” 2016, [Online]. Available: https://www.math.upenn.edu/~deturck/m425/m425-dalembert.pdf.