Integer Linear Programming Formulations for the RCPSP considering Multi-Skill, Multi-Mode, and Minimum and Maximum Time Lags

Abstract

The project scheduling problem is essential both in
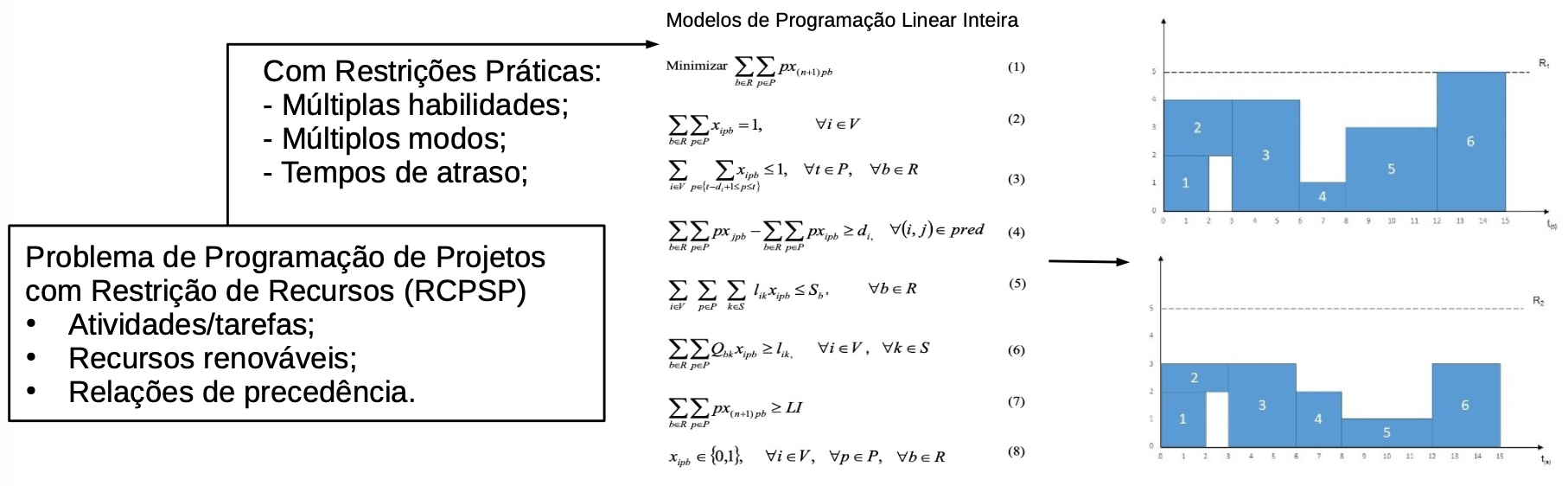
the theoretical part, as in the field of operational research, and practice, with the project management in corporate environments. Integer linear programming formulations indexed on time are
studied for the Resource-Constrained Project  Scheduling Problem (RCPSP). Moreover, the multi-skill, multiple modes, and time lag constraints are taken into consideration. The objective of the RCPSP is to minimize the makespan. The formulations are solved with the default branch-and-cut algorithm of the solver Gurobi Optimizer. The formulations and solver are analyzed concerning the runtime, the number of optimal solutions, and the gap on the
resolution of more than 2000 instances. Results indicate the solver can have better performance when instances with up to 50 activities are solved. Then, to develop models to handle hard instances of this problem is a challenge. Moreover, it can bring
significant advantages to the corporate environment, helping managers to make accurate decisions and reduce costs.