Local Adaptive Bivariate Shrinkage Function for Seisogram Wavelet Based Denoising
Keywords:
signal denoising, discrete wavelet transform, geophysical signal processingAbstract
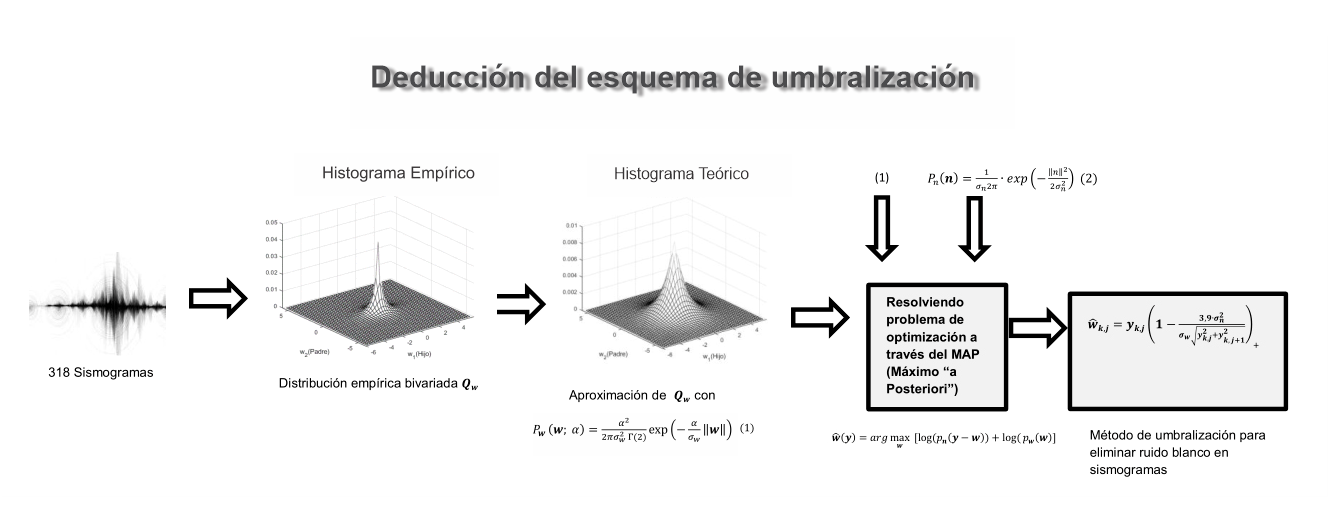
This paper presents an effective and wavelet-based seismogram denoising algorithm that considers the dependencies between the wavelet coefficients and their parents. For this purpose, a non-Gaussian bivariate distributions is used and corresponding nonlinear threshold function (shrinkage function) is derived using Bayesian estimation theory, in particular the “maximum a posteriori” estimator. To evaluate the performance of the proposed algorithm, the method is applied to seismograms that are corrupted with additive Gaussian noise over a wide range of noise variance. Experimental results are compared with different denoising schemes. The experimental results indicate that the proposed method not only outperforms the other denoising algorithms in terms of SNR but also helps retain other important information like the P-phase onsets.
Downloads