Reversibility for Quantum Programming Language QML
Keywords:
qml, Quantum computation, quantum programming, programming language, reversibilityAbstract
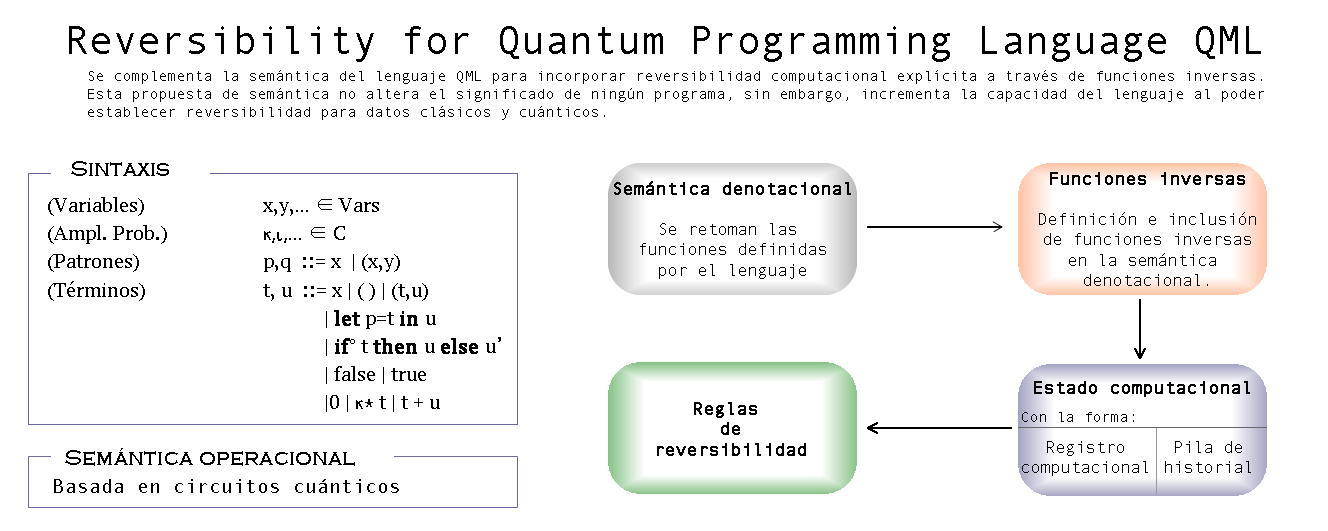
We present an extension of the denotational semantic model of the quantum programming language QML, to which computational reversibility is incorporated. The semantics of QML is defined in a functional setting which consider classical and quantum data, to which we add inverse functions. Additionally we incorporate into the semantics a history track which allows reversibility in QML. From the generation and processing of the history track and the final result of a program, the rules for executing reversibility allow to compute the original input data. This work contributes to the study of reversibility in quantum programming languages and considering that there is not yet a quantum computer in which the language can be implemented, this history and the proposed inverse functions are not trivial and allows us to determine that this language is reversible.
Downloads
References
M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2010.
P. W. Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” 1994.
M. Ying, Foundations of Quantum Programming, 1st ed. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 2016.
R. J. Lipton and K. W. Regan, Quantum Algorithms via Linear Algebra: A Primer. The MIT Press, 2014.
J. A. Miszczak, “High-level structures for quantum computing,” Synthesis Lectures on Quantum Computing, vol. 4, 05 2012.
J. Palsberg, “Toward a universal quantum programming language,” XRDS: Crossroads, The ACM Magazine for Students, vol. 26, pp. 14–17, 09 2019.
W.-L. Chang and A. V. Vasilakos, Fundaments of Quantum Programming in IBM’s Quantum Computers. Springer International Publishing, 01 2021.
B. O¨ mer, “A procedural formalism for quantum computing,” AIP Conference Proceedings, vol. 627, no. 1, p. 276, 2002.
H. Mlnar’k, “Quantum programming language LanQ,” September 2007.
J. W. Sanders and P. Zuliani, “Quantum programming,” in Mathematics of Program Construction, R. Backhouse and J. N. Oliveira, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2000, pp. 80–99.
S. J. Gay, “Quantum programming languages: Survey and bibliography,” Mathematical. Structures in Comp. Sci., vol. 16, no. 4, pp. 581–600, 2006.
P. Jorrand and M. Lalire, From Quantum Physics to Programming Languages: A Process Algebraic Approach. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005, pp. 1–16.
P. Selinger, “A brief survey of quantum programming languages,” in In Proceedings of the 7th International Symposium on Functional and Logic Programming. Springer, 2004.
——, “Towards a semantics for higher-order quantum computation,” in Proceedings of the 2nd International Workshop on Quantum Programming Languages, 2004, pp. 127–143.
M. Lampis, K. G. Ginis, M. A. Papakyriakou, and N. S. Papaspyrou, “Quantum data and control made easier,” Electron. Notes Theor. Comput. Sci., vol. 210, pp. 85–105, Jul. 2008.
P. Fu, K. Kishida, and P. Selinger, “Linear dependent type theory for quantum programming languages,” 2020.
P. Sestoft, Programming Language Concepts. Springer, 01 2017.
A. v. Tonder, “A lambda calculus for quantum computation,” SIAM J. Comput., vol. 33, no. 5, pp. 1109–1135, 2004.
J. J. Grattage, “A functional quantum programming language,” 2006.
T. Altenkirch, J. Grattage, J. K. Vizzotto, and A. Sabry, “An algebra of pure quantum programming,” Electronic Notes in Theoretical Computer Science, vol. 170, pp. 23 – 47, 2007, proceedings of the 3rd International Workshop on Quantum Programming Languages (QPL 2005).
T. Altenkirch and J. Grattage, “A functional quantum programming language,” in 20th Annual IEEE Symposium on Logic in Computer Science (LICS’ 05), June 2005, pp. 249–258.
J. Carette, C.-H. Chen, V. Choudhury, and A. Sabry, “From reversible programs to univalent universes and back,” Electronic Notes in Theoretical Computer Science, vol. 336, pp. 5 – 25, 2018, the Thirtythird Conference on the Mathematical Foundations of Programming Semantics (MFPS XXXIII).
R. Wille, E. Sch¨onborn, M. Soeken, and R. Drechsler, “Syrec: A hardware description language for the specification and synthesis of reversible circuits,” Integration, the VLSI Journal, vol. 53, 11 2015.
D. McMahon, Quantum Computing Explained. John Wiley & Sons, 2007.
P. Selinger, “A finite alternation result for reversible boolean circuits,” Science of Computer Programming, vol. 151, p. 2–17, Jan 2018. [Online]. Available: http://dx.doi.org/10.1016/j.scico.2017.08.011
R. Landauer, “Irreversibility and heat generation in the computing process,” IBM Journal of Research and Development, vol. 5, no. 3, pp. 183–191, July 1961.
N. Nishida, A. Palacios, and G. Vidal, “Reversible computation in term rewriting,” Journal of Logical and Algebraic Methods in Programming, vol. 94, pp. 128 – 149, 2018.
S. Abramsky, “A structural approach to reversible computation,” Theoretical Computer Science, vol. 347, no. 3, pp. 441 – 464, 2005.
C. H. Bennett, “Logical reversibility of computation,” IBM J. Res. Dev., vol. 17, no. 6, pp. 525–532, 1973.
J. Preskill, Lecture Notes for Physics 229:Quantum Information and Computation. CreateSpace Independent Publishing Platform, 2015.
R. Gl¨uck and R. Kaarsgaard, “A categorical foundation for structured reversible flowchart languages,” Electronic Notes in Theoretical Computer Science, vol. 336, pp. 155 – 171, 2018, the Thirty-third Conference on the Mathematical Foundations of Programming Semantics (MFPS XXXIII).
A. S. Green and T. Altenkirch, “From reversible to irreversible computations,” Electronic Notes in Theoretical Computer Science, vol. 210, pp. 65 – 74, 2008, proceedings of the 4th International Workshop on Quantum Programming Languages (QPL 2006).
A. D. Vos, “Reversible computer hardware,” Electronic Notes in Theoretical Computer Science, vol. 253, no. 6, pp. 17 – 22, 2010, proceedings of the Workshop on Reversible Computation (RC 2009).
A. B. Matos, “Linear programs in a simple reversible language,” Theoretical Computer Science, vol. 290, no. 3, pp. 2063 – 2074, 2003.
T. Yokoyama, “Reversible computation and reversible programming languages,” Electronic Notes in Theoretical Computer Science, vol. 253, no. 6, pp. 71 – 81, 2010, proceedings of the Workshop on Reversible Computation (RC 2009).
C. Heunen and M. Karvonen, “Reversible monadic computing,” Electronic Notes in Theoretical Computer Science, vol. 319, pp. 217 – 237, 2015, the 31st Conference on the Mathematical Foundations of Programming Semantics (MFPS XXXI).
L. Paolini, M. Piccolo, and L. Roversi, “A class of reversible primitive recursive functions,” Electronic Notes in Theoretical Computer Science, vol. 322, pp. 227 – 242, 2016, proceedings of ICTCS 2015, the 16th Italian Conference on Theoretical Computer Science.
E. Moggi, “Computational lambda-calculus and monads,” in Proceedings of the Fourth Annual Symposium on Logic in Computer Science. IEEE Press, 1989, pp. 14–23.
S. Awodey, Category Theory, ser. Oxford Logic Guides. Oxford University Press, 2006.