Reducing the Number of Control Actions in the Discrete Reactive Optimal Power Flow
Keywords:
Optimal Power Flow problem, complementarity constraints, discrete variablesAbstract
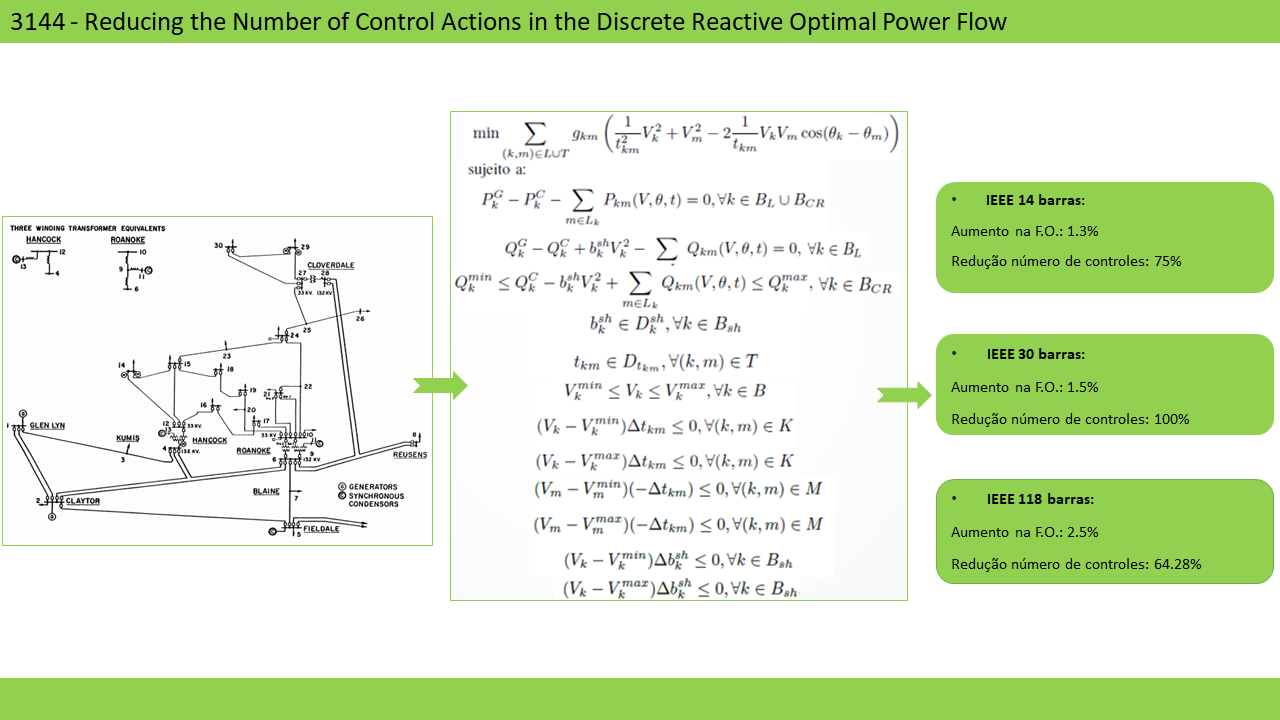
This paper proposes a new formulation for the Discrete Reactive Optimal Power Flow problem (DROPF) that aims at reducing the number of control actions of the problem. For such a purpose, additional constraints are introduced in the classical model to the DROPF problem so as to represent specific behaviors of voltage control devices in the electrical system. These behaviors involve the actuation of a control device only when the voltage magnitude limit of the bus controlled by such device is effectively reached. The proposed DROPF model is solved by the branch-and-bound method implemented in the free solver BONMIN. Numerical tests were performed using the IEEE 14, 30 and 118 bus electrical systems and demonstrated the efficiency of the proposed model. The results are compared with the ones obtained by a classical DROPF.
Downloads
References
A. J. Monticelli, Fluxo de carga em redes de energia elétrica, E. Blucher, 1983.
J. A. Delgado et al., "A Modified Barrier and Barrier Method and the Optimal Power Flow Problem," IEEE Lat. Am. Trans., vol. 1, no. 9, pp. 1629-1638, 2017.
J. Carpentier, "Contribution a l’etude du dispatching economique," Bull Soc Francaise Electr., vol. 8, pp. 431-447, 1962.
H.W. Dommel andW. F. Tinney, "Optimal power flow solutions," Trans. Power Appar. Syst., no. 10, pp. 1866-1876, 1968.
D. I. Sun et al., "Optimal power flow by Newton approach," Trans. Power Appar. Syst., no. 10, pp. 2864-2880, 1984.
R. C. Burchett, H. H. Happ and D. R. Vierath, "Quadratically convergent optimal power flow," Trans. Power Appar. Syst., no. 11, pp. 3267-3275, 1984.
G. L. Torres and V. H. Quintana, "On a nonlinear multiple-centralitycorrections interior-point method for optimal power flow," IEEE Trans. Power Syst., vol. 16, no. 2, pp. 222-228, 2001.
W. -HE. Liu, A. D. Papalexopoulos and W. F. Tinney, "Discrete shunt controls in a Newton optimal power flow," IEEE Trans. Power Syst., vol. 7, no. 4, pp. 1509-1518, 1992.
A. G. Bakirtzis, P. N. Biskas, C. E. Zoumas, and V. Petridis, “Optimal power flow by enhanced genetic algorithm,” IEEE Trans. Power Syst., vol. 17, no. 2, pp. 229–236, 2002.
M. M. Adibi, R. A. Polyak, I. A. Griva, and L. Mili, “Optimal transformer tap selection using modified barrier-augmented Lagrangian method,” IEEE Trans. Power Syst., vol. 18, no. 1, pp. 251–257, 2003.
L. Liu, X. Wang,X.Ding, andH.Chen, “A robust approach to optimalpower flow with discrete variables,” IEEE Trans. Power Syst., vol. 24, no. 3, pp. 1182–1190, 2009.
C. R. N. Estevam et al., "Reactive power dispatch and planning using a non-linear branch-and-bound algorithm," IET Gen., Transm., Distrib., vol. 4, no. 8, pp. 963-973, 2010.
D. T. Phan, "Lagrangian duality and branch-and-bound algorithms for optimal power flow," Operations Research, vol. 60, no. 2, pp. 275-285, 2012.
M. C. A. Silva and E. A. Belati, "Allocation of static VAr compensators using optimal reactive power flow and branch & bound algorithm," IEEE Lat. Am. Trans., vol. 14, no. 5, pp. 2194-2200, 2016.
F. Capitanescu, W. Rosehart and L. Wehenkel, "Optimal power flow computations with constraints limiting the number of control actions," in 2009 IEEE Bucharest PowerTech, IEEE, 2009, pp. 1-8.
F. Capitanescu et al. "State-of-the-art, challenges, and future trends in security constrained optimal power flow," Electr. Power Syst. Res., vol. 81, no. 8, pp. 1731-1741, 2011.
E. M. Soler, E. N. Asada and G. R. M. Costa,"Penalty-based nonlinear solver for optimal reactive power dispatch with discrete controls," IEEE Trans. Power Syst., vol. 28, no. 3, pp. 2174-2182, 2013.
G. G. Lage, "O fluxo de potência ótimo reativo com variáveis de controle discretas e restrições de atuação de dispositivos de controle de tensão," Ph.D. dissertation, Dep. de Eng. Elétrica e Computação, Universidade de
São Paulo, São Carlos, SP, 2013.
W. Rosehart, C. Roman and A. Schellenberg, "Optimal power flow with complementarity constraints," IEEE Trans. Power Syst., vol. 20, no.2, pp. 813-822, 2005.
P. Bonami et al., "An algorithmic framework for convex mixed integer nonlinear programs," Discrete Optimiz., vol. 5, pp. 186-204, 2008.
P. Bonami and J. Lee, "BONMIN User’s Manual", Numer Math, vol. 4, pp. 1-32, 2007.
A. Gomez-Exposito, A. J. Conejo and C. Canizares, Electric energy systems: analysis and operation, CRC press, 2018.
R. Christie, Power System Test Case Archive. Washington University, 2013, Disponível em: <http://labs.ece.uw.edu/pstca/>. Acesso em: 01 Jun. 2018.