Comparison Between Linear and Tensor Models of EEG Signals

Abstract

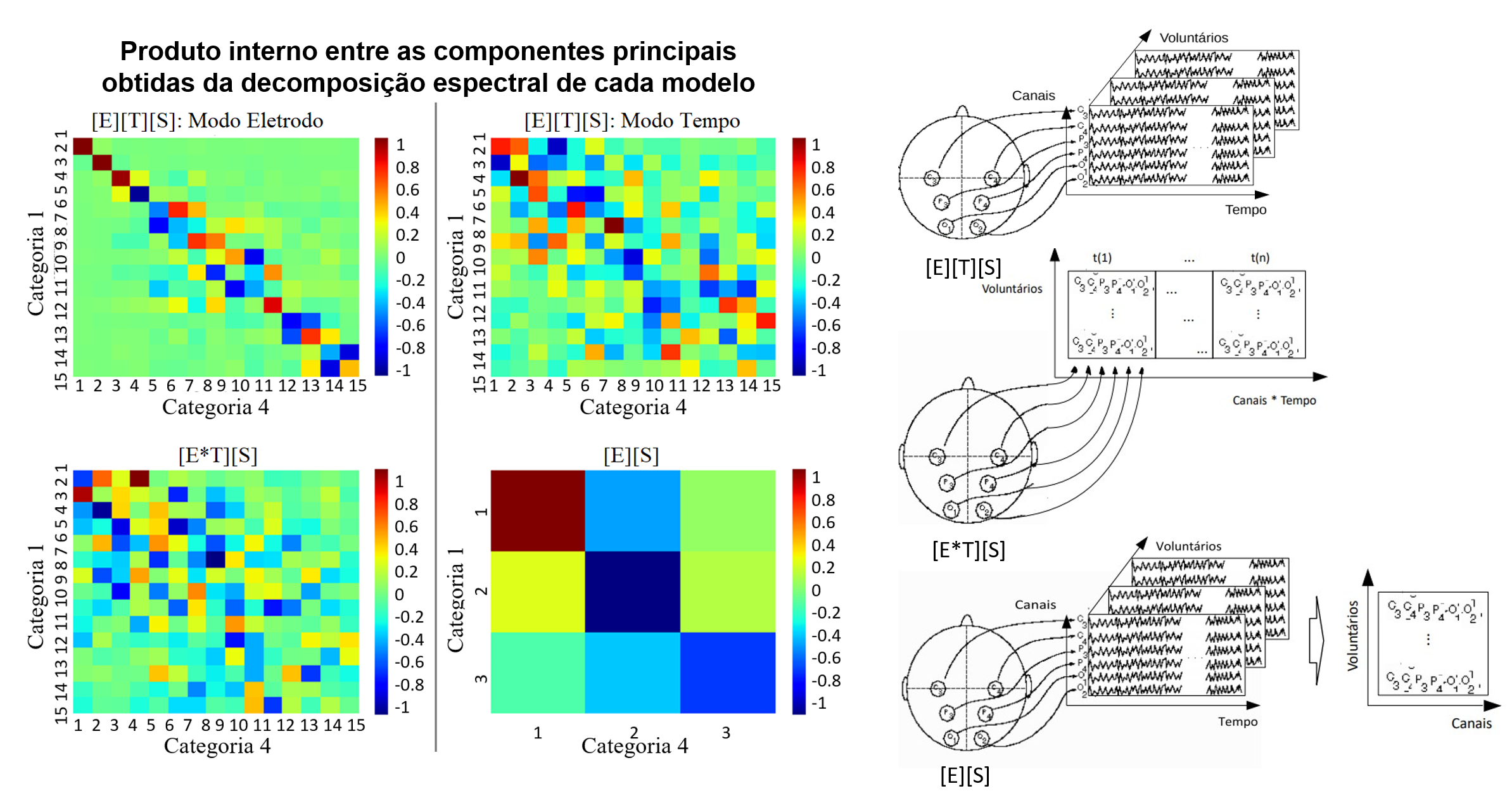
Electroencephalography (EEG) is an important tool for the study of the human brain because it provides potentially useful signals for understanding the spatial and temporal dynamics of neural information processing. These signals are commonly represented by vector or matrix structures, which may counteract their natural demand for a multidimensional representation. Thus, in this case, the information from an EEG signal should be represented using tensors. This study presents a discussion of how these different mathematical structures can be harnessed to obtain functional brain information. Two matrix models and one tensor model were used to produce topographic maps and the classification of brain patterns. We use principal component analysis, correlation entropy, and the Generalized Low Rank Approximations of Matrices to reduce the dimensionality and feature extraction of each model, respectively. The acquisition of EEG signals was done in another author's experiment involving the chess game. Our results show at least three different and complementary ways for the representation of cognitive brain maps and, as far as the classification of these data is concerned, the tensorial model stands out in terms of the level of compression and precision.